Mala
škola
kristalografije
Digitalni
udžbenik
za znatiželjne učenike srednjih škola
Recenzenti
Prof. dr. sc. Dubravka
Matković-Čalogović
Prof. dr. sc. Stanko Popović
Fotografije
i crteži
Milan Sikirica
Udžbenik je besplatan.
Nastao je
nesebičnim radom autora i recenzenata. Zato se ni jedan dio ovog
udžbenika ne
smije ni u kojem obliku i na bilo koji način koristiti u komercijalne
svrhe.
Dozvoljeno je korištenje za osobne potrebe i za nastavu u školama.
Slobodno
smijete besplatno umnožavati, dijeliti, distribuirati i prerađivati
ovaj
udžbenik za potrebe nastave uz obvezno citiranje izvornika. Sva su
autorska
prava zadržana.
U
spomen na našeg učitelja akademika Draga Grdenića (1919.
- 2018.),
jednog od osnivača "Instituta Ruđer Bošković", koji je u
Hrvatskoj prvi
primijenio metodu rendgenske difrakcije za određivanje kristalnih i
molekulskih struktura te utemeljio Zagrebačku školu strukturne kemije
koja danas zauzima značajno mjesto u europskoj znanosti.
3. Morfološke
karakteristike kristala
3.1. Simetrijski
elementi kristala
3.3. Označavanje ploha
na kristalu
3.4. Millerovi indeksi
kristalnih ploha
3.6. Kristalni razredi
ili kristalne klase
4.2. Bravaisove
prostorne rešetke
4.3. Prostorne grupe
simetrije
4.4. Slagaline kuglica
jednake veličine
4.4.1. Primitivna
(jednostavna) kubna rešetka
4.4.2. Prostorno
centrirana kubna rešetka
4.4.3. Plošno
centrirana kubna rešetka
4.4.4. Heksagonska
gusta slagalina
5.1. Otkriće i svojstva
X-zraka
5.2. Difrakcija
rendgenskih zraka
5.3. Kristalna rešetka
i mrežne ravnine
5.4. 2. Struktura
natrijeva klorida
5.4.3. Valna duljina
rendgenskih zraka
5.5. Svojstva
rendgenskih zraka
5.5.2. Izvori
rendgenskih zraka
6. Rendgenska
strukturna analiza
6.1. Intenzitet
difrakcijskih maksimuma
6.3. Raspodjela
elektronske gustoće
7.
Debye-Scherrer-Hull-ova metoda
7.1. Identifikacija
kemijskog spoja
7.2. Indiciranje
difrakcijskih slika
Preporučena
literatura za daljnje čitanje i učenje:
Predgovor
Svojedobno se
u srednjim školama učila astronomija. Onda je "došla" reforma
obrazovanja pa su astronomiju ukinuli. Bilo je to poslije Drugoga
svjetskoga
rata, upravo kad je na Mount Palomaru, Kalifornija, 1947. godine
montiran
najveći teleskop na svijetu sa zrcalom promjera 200 inča (5,08 m).
Danas, samo
sedamdesetak godina poslije, istražuje se daleki svemir, traže se novi
planeti
pogodni za život i planiraju putovanja na Mars. Istodobno umjesto za
astronomiju kod nas se razvijao interes za astrologiju pa danas nema
novina ili
časopisa bez dnevnog, tjednog ili bilokakvog horoskopa, a u kasnim
noćnim
satima lokalnim TV postajama gospodare astrolozi, vidovnjaci, proroci,
gatare,
iscjelitelji i slične spodobe.
Na
Kemijskom odjelu Srednje tehničke škole industrijskog smjera još sam
1949. godine
imao predmet mineralogija s nešto malo geologije. No, "reformatori"
su i nju pomeli. Mineralogija je utopljena u kemiju, a geologija u
zemljopis, tj.
geografiju. Bilo je to u doba neslućenih otkrića temeljenih na
kristalografji:
1945. kristalna
struktura penicilina,
1947. otkriće tranzistora, 1950. rast kristala germanija i silicija iz
taline
za potrebe istraživanja i proizvodnje poluvodiča, 1958. kristalna
struktura
mioglobina, 1960. rubinski laser, III-V poluvodiči itd. Istodobno, kod
nas se umjesto
kristalografije razvila kristaloterapija, što će reći liječenje
kristalima
različitih minerala kojima su pripisana natprirodna svojstva. Tako je
zapostavljanje znanosti omogućilo širenje neznanja i pseudoznanja, a
šarlatanima omogućilo izvlačenje novca od neukog naroda.
Tomu se
možemo suprostaviti samo širenjem znanja. No, kako u aktualnoj "reformi
obrazovanja" kristalografija nije zauzela neko zavidno mjesto, odlučio
sam
napisati Malu školu kristalografije. Namijenjena je učenicima i
njihovim
nastavnicima, ali i roditeljima. Kristalografija je bitna za razvoj
mnoštva
novih materijala: za elektroniku, računala, dijelove automobila,
zrakoplova, lijekova,
farmaceutsku industriju, pa i za kozmetiku. Danas se ne može
patentirati neki
lijek bez znanja o njegovoj kristalnoj strukturi i načinu na koji
djeluje na bakterije
koje napadaju naše stanice. Kristalografija omogućuje razlikovanje
strukture
molekula istoga kemijskog sastava. Sjeća li se netko Talidomida
koji je u vremenu od 1957. do 1961.
godine uzrokovao
jednu od najvećih medicinskih tragedija modernih vremena, kad je zbog
primjene
toga lijeka rođeno oko 10.000 do 20.000 djece s teškim urođenim manama.
Talidomid
je smjesa lijevog i desnog enantiomera, od kojih samo jedan
uzrokuje urođene mane. Da je u istraživanje Talidomida bila uključena
kristalografija, do tragedije vjerojatno ne bi došlo.
Danas
živimo u informatičkom dobu koje je omogućila upravo kristalografija.
Sva
računala, tableti, mobiteli, LED rasvjeta, solarni paneli, litij-ionske
baterije, TV i "šta
ti ga ja znam
što sve još", temelje se na iskorištavanju svojstava kristala. Vlasnici
pametnih telefona (mobitela) nisu svjesni da, zahvaljujući kristalima, u džepu nose moćno
računalo.
Unatoč
tomu, još prije nekoliko mjeseci mogli smo u dnevnim tiskovinama čitati
da
mobiteli, tableti i računala koji, "osim što štete zdravlju", dovode
i do "otuđenja" jer djeca više međusobno ne komuniciraju. Zar je to
zaista tako?. Naprotiv, djeca i odrasli međusobno još više komuniciraju
nego ikad
prije, samo se način komunikacije promijenio. Zahvaljujući
kristalografiji i
kristalima danas možemo ne samo razgovarati već i vidjeti sugovornika
ma gdje
se on u tom trenutku nalazio. Zar to nije divno. Tko još čeka da mu
poštar
donese pismo, telegram ili fotografiju rođaka koji je prije više
desetaka
godina otišao primjerice u Australiju?
Dok se u
svim oblastima ljudske djelatnosti uvodi informatizacija, digitalne tehnologije i robotika, a
znanstvenici razvijaju bioničke
proteze i umjetnu inteligenciju, kod nas svjedočimo višegodišnjim
nevjerojatnim
otporima bilo kakvoj promjeni koja bi dovela do unapređenja nastavnih
metoda,
oblika rada i digitalizaciji obrazovnih sadržaja. Sjećate li se koliko
je još
prije samo godinu dana bilo "frke" oko informatizacije škola,
digitalizacije nastavnih sadržaja i drugog. Svi su bili protiv jer
"uporabom
digitalne tehnologije mi stvaramo generacije rastresene djece. U prekratkom vremenu
djeca dobivaju previše
informacija, ne prerade ih i tu je velik dio problema s učenjem". ???.
A onda je
"došao"
COVID-19,
tj. korona virus i učenje na daljinu. Ništa novo. I
prije je postojalo dopisno obrazovanje, samo se promijenila
tehnologija. I
prije su postojali korona virusi, ali ovaj je mutirao (lat. mutare -
mijenjati)
i prisilio nas da "navrat-nanos" mijenjamo nastavne strategije, metode,
sadržaje i oblike nastavnog rada. Očito, zaboravili smo, ili nismo
htjeli
znati, da u svim prirodnim i društvenim procesima vrijedi zakon
evolucije (lat.
evolutio - razvoj, razvitak). Zato
nastavne
metode, oblici rada i sadržaji đačke torbe moraju stalno evoluirati.
Tehnologije i društva koja ne evoluiraju, zaostaju i nestaju s lica
Zemlje.
"Stalna na tom svijetu samo mijena jest" - za sada.
Sjetih se
tako jedne davne rasprave o obrazovanju na kojoj je akademik Zvonimir
Devidé, (1921. - 2011.), naš
istaknuti biolog i botaničar načinio sljedeću usporedbu: "Pramajmun koji
nije znao procijeniti granu na koju skače potencijalno je bio mrtav
majmun, nije
imao potomaka i prestao je biti karika u lancu evolucije".
Autor
1. Uvod
Tijekom
cijele povijesti ljude je fascinirala ljepota i tajnovitost kristala.
Riječ
kristal potječe od grčke riječi krystallos
što znači čisti led. Ta se riječ uglavnom odnosila na kvarc.
U 19. stoljeću
Bogoslav
Šulek predlagao je
da se umjesto kristal rabi riječ ledac. Taj se naziv za
kristale u nas zadržao još u prvoj polovini 20. stoljeća. No, danas je
gotovo
zaboravljen. Prvi zapisi o mineralima (franc. minéral - ruda) i
kristalima, osobito dragom kamenju, potječu još iz Babilona, drevne
Kine, te drevne
Indije. Jedan od
prvih pisanih radova drevnoga grčko-rimskoga svijeta jest rad
Aristotelova
učenika Teofrasta
(370. – 285.
pr. Kr.) u kojem je po prvi put opisano pedesetak minerala, pretežno
dragoga
kamenja. Plinije
stariji (23. - 79.)
divio se pravilnim šesterostranim prizmama kristala
kvarca, a u svojoj knjizi Naturalis
Historia
opisuje
mnoge minerale i objašnjava njihova svojstva. Raspravljajući o oblicima
kristala,
posebno dijamanta u obliku oktaedra, položio je temelje kristalografije. U to doba
u drevnoj Indiji i Kini bio je poznat postupak kristalizacije šećera i
soli. U
ranom srednjem vijeku u Egiptu i Španjolskoj ovladali su tehnikom
rezanja kristala
radi ukrašavanja predmeta. Njemački liječnik i rudar Georg Bauer,
poznatiji kao
Georgius
Agricola (1494. –
1555.), svojim djelima kao što su De re
metallica
(1556.) i De Natura
Fossilium
(O prirodi
stijena, 1546.), potaknuo je znanstveni pristup mineralima, rudama i
stijenama
pa ga se može smatrati začetnikom znanstveno utemeljene mineralogije.
Engleski
kemičar Robert
Boyle (1627. –
1691.) u svojoj knjizi The
Sceptical Chymist (1661.) koristio je riječ kristal u općem
smislu, ne
ograničavajući se samo na kristale kvarca. Godine 1672. objavio je
knjigu o
podrijetlu i svojstvima dragulja te je uočio stalnost oblika pojedinih
vrsta
kristala, ali nije uočio stalnost kutova među plohama. Poput Steno-a,
također je vjerovao da su kristali
rasli iz otopine uzastopnim slaganjem slojeva čestica. Također je uočio
lamelnu
građu mnogih minerala i napravio seriju bilježaka o oblicima kristala. Sustavne znanstvene studije
minerala i stijena nastavljene
su i u post-renesansnoj Europi.
Pritom je važnu
ulogu imao izum mikroskopa u 17.
stoljeću. Otkriće rendgenskih zraka 1895. godine omogućilo je
prekretnicu u
načinu proučavanja stijena i minerala. Laue, Fridrich, Knipping, otac i
sin
Bragg i još mnogi poslije njih, "upalili su novo svjetlo" koje je
omogućilo pogled u unutarnju građu kristala.
1.1. Litosfera
Zemlja se
sastoji od četiri omotača: atmosfere, hidrosfere, biosfere i
litosfere. Litosfera
je vanjski
tvrdi kameni omotač Zemlje koji seže do dubine oko 200 km. Sastoji od
tri grupe
stijena:
eruptivnih, sedimentnih i metamorfnih. Stijene se razlikuju po načinu
postanka,
mehaničkim svojstvima, kemijskom sastavu i boji. Eruptivne ili
magmatske
stijene nastale su kristalizacijom ili skrućivanjem magme, odnosno lave. Najpoznatije eruptivne
stijene su granit, bazalt i gabro. Sedimentne stijene nastale su
taloženjem ostataka drugih stijena: pijeska, šljunka ili gline. Metamorfne
stijene nastale su
preobrazbom eruptivnih i sedimentnih stijena pod utjecajem
visokog tlaka i temperature. Najpoznatija metamorfna stijena je mramor koji je nastao metamorfozom vapnenca, a
vapnenac je sedimentna organogena stijena nastala taloženjem ljuštura
izumrlih
morskih organizama. Stijene su mješavine minerala.
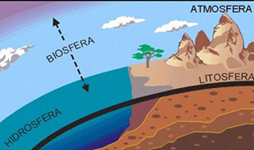
Slika
1.1. Shematski
prikaz Zemljinog omotača
Izvor:http://ritahsmarques.wixsite.com/ritaportefoliocn/sobre-1-c1aob
1.2. Minerali
Minerali su prirodne homogene krute tvari definiranoga kemijskog sastava koji se može izraziti kemijskom formulom. Odlikuju se stalnim fizičkim svojstvima i pravilnom unutarnjom građom koja se može opisati kristalnom rešetkom. Prema postanku, minerali mogu biti magmatskog, sedimentnog ili metamorfnog podrijetla. Rudni minerali su oni koji sadržavaju metale. Velika ležišta takvih minerala nazivaju se rudama te se iskorištavaju za industrijsko dobivanje metala.
Petrogeni
minerali (grč.-lat.
petra - stijena, genesis -
postanak) izgrađuju stijene. Stijene
su mineralni agregati (lat. aggregare -
nagomilati), odnosno krute i
guste nakupine sitnih kristalića različitih minerala. Primjerice, granit (lat. granum -
zrno) je čvrsta stijena magmatskog podrijetla koja se
najčešće sastoji od kristalića kvarca, SiO2, biotita
- K(Mg,Fe)3AlSi3O10(F,OH),
minerala koji pripada skupini tinjaca, i glinenaca
ili
feldspata (njem. Feldspat). Po
kemijskom
sastavu glinenci su natrijevi, kalcijevi ili kalijevi alumosilikati.
Glinenci
čine više od 60 % Zemljine kore.

Slika 1.2.
Granit
Granit se
rabi kao građevinski materijal. Može ga se vidjeti u obliku podnih
pločica, obloga pročelja zgrada, nadgrobnih spomenika, ili kockica
kojima su
popločeni starinski trgovi i neke ulice, primjerice Markov trg,
Mesnička i Radićeva
ulica u Zagrebu.

Slika 1.3. Uzorci minerala: a) ametist - SiO2, b) rumenica - HgS, c) Rutil - TiO2
2.
Kristalografija
Kristalografija
je znanost o nastanku, obliku, simetriji, strukturi i
svojstvima kristala. Njemački matematičar, astronom i astrolog Johannes Kepler (1571. – 1630.)
divio se pravilnim šesterokutnim pahuljama snijega na svom kaputu. On
je 1611.
napisao prvi "matematički opis kristala" (lat. naslov: Strena
Seu de Nive Sexangula). Pritom se
pita zašto snježne pahulje uvijek imaju šest vrhova? Zašto snježne
pahulje ne
padaju sa pet ili sedam vrhova?

Slika
2.1. Johannes
Kepler i njegove slagaline kuglica jednake veličine
Izvori: http://bit-player.org/2012/keplers-snowflake
https://en.wikipedia.org/wiki/Kepler_conjecture
Jedno od
njegovih glavnih otkrića bila je geometrija najgušćega slaganja
kuglica jednake veličine kojim je pokazao kako se gustim slaganjem
malih
kuglica leda mogu dobiti šesterokutne snježne pahuljice, a nikada
petero ili
sedmerokutne. Keplerov rad o šesterokutnim kristalima
snijega može se
smatrati pretečom otkrića zakona o stalnosti kuta među plohama
kristala. (N.
Steno, 1669; M.V. Lomonosov, 1749; Romé de l'Isle, 1783; R.J. Haüy,
1784; E.S.
Fjodorov, 1885.).
Problemom
najgušćega slaganja kuglica jednake veličine više se bavio
britanski fizičar, matematičar i izumitelj Robert Hook
(1635. –
1703.) poznat po Hookovom zakonu iz mehanike. Promatrajući mikroskopom
komadiće
kristala kvarca,
dobivene
lomljenjem većih kristala, na površini prelomljenih komadića uočio je
plohe
različita geometrijskog oblika. Kako nastaju ti pravilni geometrijski
likovi
pokušao je objasniti slaganjem kuglica u najgušće slojeve. Primjerice,
tri
kuglice mogu oblikovati jednakostranični trokut, četiri mogu oblikovati
romb, a
pet kuglica može formirati trapez. Hook je također tvrdio da četiri
kuglice
mogu formirati tetraedar, ali nije opisao druge trodimenzijske
strukture.
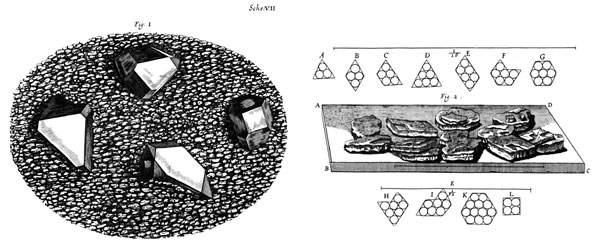
Slika
2.2. Hook-ove
slagaline kuglica jednake veličine
Izvor: https://hookelabs.com/about/aboutRobertHooke.html
Danski
anatom i geolog Niels Stensen, poznatiji
po latiniziranom imenu Nicolaus Stenonius, ili Nicolaus Steno, uočio je
1669.
godine jedan od osnovnih zakona kristalografije. Na temelju studija
velikog
broja kristala kvarca ustanovio je da su na svakom kristalu kvarca
kutovi
između odgovarajućih ploha uvijek jednaki, bez obzira na veličinu i
podrijetlo
kristala.

Slika
2.3. a) Niels
Stensen (1638. – 1686.), b)
Jean-Baptiste
L. Romé de l'Isle (1736. – 1790.)
Izvori: https://en.wikipedia.org/wiki/Nicolas_Steno
http://www.xtal.iqfr.csic.es/Cristalografia/parte_01_1-en.html
Steno i
drugi mineralozi uočili su stalnost kutova među plohama
minerala kao što su kvarc, kalcit i pirit. No, francuski mineralog Jean-Baptiste
L. Romé de l'Isle
1772. godine ustvrdio je da svi kristali iste
tvari, bez obzira na njihov različit izgled ili nalazište, uvijek imaju
istu
geometrijsku formu i pokazuju istovjetne kutove između pojedinih
kristalnih
ploha. To je svojstvo karakteristično za kristale svake tvari te je
poznato kao
zakon stalnosti kutova ili prvi zakon kristalografije.
Taj
se zakon često naziva i Stenoovim
zakonom. Romé de l'Isle bio je uvjeren da se minerali mogu
sistematizirati
na osnovi njihove forme te je identificirao 450 formi kristala.
Francuski
mineralog René Just
Haüy začetnik je
moderne kristalografije. Njegov interes za kristalografiju
javio se nakon što mu je u kući njegova prijatelja M. Defrance-a
slučajno ispao
i razbio se kristal kalcita. Skupljajući razbijene komadiće uočio je
sličnost
njihova oblika. Vrativši se u svoj kabinet nastavio je "razbijati"
kristale kalcita. Promatrajući fragmente uočio je da se kristali
kalcita kalaju
tako da tvore ravne plohe koje se sijeku pod stalnim kutovima.
Ustanovio je da
bez obzira na izvorni oblik dobiveni fragmenti uvijek imaju oblik
romboedra. Na temelju
prijašnjih otkrića znao je da kristali iste vrste uvijek imaju istu
geometrijsku formu i pokazuju istovjetne kutove između pojedinih
kristalnih
ploha. Na temelju tih dviju spoznaja zaključio je da su svi kristali
izgrađeni
od manjih kemijski identičnih poliedara koje je nazvao molekule
sastavljačice (franc.
molécule intégrantes).

Slika 2.4. a) René Just Haüy (1743. – 1822.). b) Fragmenti kristala kalcita imaju oblik romboedra. Doznajte više na: http://www.minsocam.org/msa/collectors_corner/arc/hauyiv.htm

Slika 2.5. Ilustracija iz Haüy-jeve knjige Essai d 'une théorie sur la structure des crystaux (1784. god.) kojom pokazuje kako slaganjem "molekula sastavljačica" nastaju različite plohe na kristalu
Haüy je
prvi uočio periodičnost unutarnje građe kristala što je opisao
u svojim knjigama (Essai
d'une théorie sur la structure des cristaux,
1784.; Traité de Minéralogie, 1801.). Pritom je
pokazao kako slaganjem kemijski identičnih građevnih jedinki, koje
imaju isti
oblik kao i sam kristal, nastaju različite ravne plohe na kristalu. Na temelju promatranja i mjerenja položaja ploha na
kristalima Haüy je otkrio i
drugi zakon kristalografije, zakon o
racionalnom odnosu parametara. Na
kristalu su moguće samo one plohe čiji se odsječci na zamišljenim osima
trodimenzijskog koordinatnog sustava odnose kao mali
cijeli brojevi ili jednostavni razlomci
(René-Just Haüy, 1784., 1801.).
Haüyeva otkrića
bila su važan događaj u kristalografiji, jer su
se do tada kristalografi uglavnom bavili morfologijom
kristala. Električna
svojstva kristala: triboelektrični i piroelektrični
efekt, otkrio je 1817. godine. Haüy je za obrazovne svrhe uveo drvene
modele
kristala. Takvi se modeli i danas rabe na predavanjima i ispitima iz
mineralogije.
3.
Morfološke karakteristike kristala
Na
kristalima kvarca mogu se uočiti plohe koje odgovaraju plohama
heksagonske prizme. Kristali halita (kuhinjska sol, NaCl) imaju oblik
kocke. Na
kristalima fluorita (kalcijev fluorid, CaF2)
mogu se uočiti plohe
oktaedra i kocke. Kristali uvijek pokazuju plohe koje odgovaraju nekom
geometrijskom tijelu, prizmi, piramidi i dr. Promatrajući bilo koji
kristal
lako je uočiti:
dvije
susjedne plohe na kristalu tvore brid,
tri
susjedne plohe na kristalu sijeku se u
jednoj točki koju zovemo vrh,
broj
ploha + broj vrhova = broj bridova + 2,
kutovi
među plohama kristala jedne te iste tvari
uvijek su jednaki (Steno-ov zakon).

Slika 3.1.
Na slici je prikazan kristal fluorita, CaF2.
Uočite na kristalu plohe kocke i oktaedra. Kako se naziva takvo
geometrijsko
tijelo? Koliko ploha, bridova i vrhova ima na idealnom kristalu
fluorita? Slika -
izvor: https://upload.wikimedia.org/wikipedia/commons/0/0d/3192M-fluorite1.jpg
Jedno od
prvih fizičkih svojstava koje
makroskopski ili pomoću ručne lupe zamjećujemo na uzorku minerala jest
njegov
vanjski izgled, odnosno habitus.
Lijepo razvijene kristale obično nalazimo u pukotinama i šupljinama
stijena,
najčešće u kamenolomima i rudnicima. No, vanjski izgled kristala ili
habitus
ovisi o uvjetima u kojima su se kristali razvijali kao što su tlak,
temperatura, dotok mineralne tvari, primjese u otopini i dr. Zbog toga
se
izgled kristala iste tvari iz različitih ležišta razlikuje. Kristali
idealnog
oblika u prirodi se nalaze vrlo rijetko. Pojedine se plohe ne moraju ni
razviti. Zbog različite brzine rasta plohe mogu biti različite veličine
pa
nastaju razvučeni kristali.
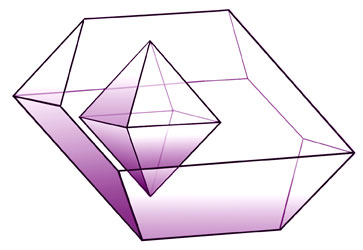
Slika 3.2.
Shematski prikaz kako iz idealanoga oktaedra nastaje razvučeni oktaedar
kad se pojedine plohe paralelno same sebi pomiču i pritom različito
povećavaju.
Obratno, od razvučenoga oblika kristala nastat će idealan oblik ako se
paralelnim pomicanjem sve paralelne plohe učine jednako velikima.
Načinite
vlastite monokristale limunske
kiseline i na njima uočite bridove i vrhove. Limunska kiselina nije
skupa te je
neškodljiva za okoliš. Potpuno je biorazgradiva. Može se nabaviti u
većim
trgovinama prehrambenih proizvoda po cijeni od oko 17 kn za 500 g.
Postupak
dobivanja monokristala limunske kiseline možete vidjeti na adresama:
https://www.youtube.com/watch?v=GH2fWrZfB3Y
https://www.youtube.com/watch?v=pyYRhvGHZvg
3.1. Simetrijski
elementi kristala
Jedno od
osnovnih svojstava koje se uočava na svim kristalima jest
simetrija (grč. symmetria - pravi
razmjer). Karakteristično svojstvo simetričnih tijela, crteža ili
ornamenata,
jest ponavljanje iste slike pošto se na njih primjeni operacija
elementa
simetrije. Na kristalima uočavamo simetrijske ravnine, simetrijske osi,
inverzijske osi i centar simetrije.
Kristal ima simetrijsku ravninu ako se nekom zamišljenom ravninom može podijeliti na dvije polovine koje se odnose kao predmet i slika u zrcalu. Takvo preslikavanje u zamišljenoj ravnini zove se operacija simetrijske ravnine. Simetrijska ravnina uvijek je paralelna s nekom od mogućih ili opaženih ploha na kristalu. Na jednom kristalu može biti više simetrijskih ravnina, ali isto tako ima kristala bez simetrijske ravnine.

Slika 3.3. Kristali kuhinjske soli i nekih drugih minerala imaju oblik kocke. Na kocki uočavamo tri međusobno okomite glavne simetrijske ravnine koje prolaze raspolovnicama nasuprotnih bridova i šest sporednih ravnina koje kocku sijeku smjerom plošnih dijagonala.

Slika 3.4. Mnoge građevine, a osobito crkve i crkveni tornjevi, građene su tako da pokazuju simetrijske elemente. Na slici je dio pročelja katedrale sv. Jakova u Šibeniku. Cijelo pročelje ima jednu simetrijsku ravninu. Izdvojite pojedine dijelove pročelja (rozete) i uočite u tim dijelovima simetrijske ravnine i simetrijske osi. (Opaska: U trenutku snimanja, 28.04.2016., na katedrali su izvođeni građevinski radovi. Uočite što nedostaje.)
Simetrijska os jest zamišljeni pravac oko kojeg se rotacijom kristala za kut 2p/n (n = 2, 3, 4, 6) vide iste plohe, bridovi i vrhovi kakvi se na kristalu (tijelu ili crtežu) vide prije rotacije. Os oko koje treba kristal zarotirati za 180o, da bi se pojavio istovrsni razmještaj ploha, bridova i vrhova, zove se digonska simetrijska os (grč. dyo - dva + gony - kut), ili digira (grč. gyros - krug), ili os drugoga reda. Os oko koje kristal treba zarotirati za 120o da bi se pojavio istovrsni razmještaj ploha, bridova i vrhova naziva se trigonska simetrijska os, trigira ili os trećega reda. Na kristalima se još pojavljuju tetragire i heksagire (grč. tettares - četiri, hex - šest).

Slika 3.5.
Kristal berila (Be3Al2Si6O18)
ima oblik heksagonske prizme. Zamislite točku na osnovki (bazi) prizme
i smjer
kojim prolazi os šestoga reda (heksagira). Iste plohe i bridovi
pojavljuju se
nakon rotacije kristala za kut 2p/6,
odnosno 60o.
Slika izvor:
http://www.johnbetts-fineminerals.com/jhbnyc/mineralmuseum/picshow.php?id=34225
Kristal
ima centar simetrije
kad se svakoj plohi na kristalu može pronaći odgovarajuća paralelna
ploha na
suprotnoj strani kristala. Možemo zamisliti jednu točku u središtu
kristala
kroz koju se preslikavaju plohe, bridovi i vrhovi kristala. Ta se točka
naziva
centrom simetrije. To znači da svaka točka na površini ili
unutrašnjosti
kristala ima svoj centrosimetrični par na jednakoj udaljenosti, ali u
suprotnom
smjeru od centra simetrije. Centar simetrije uvijek je i centar
kristala. Primjerice,
centar kocke je ujedno i centar simetrije, ali geometrijski centar ne
mora
uvijek biti i centar simetrije. Na temelju slike 3.5. zamislite i
nacrtajte
idealan kristal berila. Ima li kristal berila centar simetrije?
Za
označavanje simetrijskih elemenata kristala rabe se sljedeći
grafički simboli:

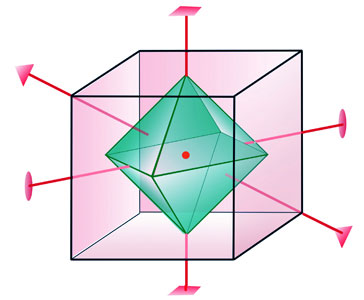
Slika 3.6. Na kocki i oktaedru, koji imaju najveći broj simetrijskih elemenata, uočavamo tri osi četvrtoga reda koje prolaze središtima nasuprotnih ploha. Četiri osi trećega reda prolaze smjerom prostorne dijagonale kocke. Šest osi drugoga reda prolazi raspolovnicama nasuprotnih bridova.

Slika 3.7. Inverzijska os četvrtoga reda uključuje rotaciju za 90o i inverziju, odnosno preslikavanje kroz zamišljenu točku koja se nalazi na toj osi.

Slika 3.8. Pred vama su crteži dvaju tetraedara. Odgovorite na sljedeća pitanja
1. Ima li tetraedar centar simetrije?
2. Nabrojite sve simetrijske ravnine i simetrijske osi koje ste uočili na tetraedru i usporedite ih s brojem simetrijskih ravnina i simetrijskih osi na kocki i oktaedru.
3. Jesu li ova dva tetraedra jednaka ili različita? Ako su jednaki, kako ćete to dokazati? Ako su različiti, u odnosu na što se oni razlikuju?
4. Građa molekule metana može se prikazati tetraedrom s atomom ugljika u središtu i atomima vodika na vrhovima. Nabrojite sve simetrijske elemente koje uočavate na molekuli metana.
5. Ima li molekula metana inverzijske osi i kojega su reda?
Doznajte
više na:
http://geol.pmf.hr/~dtibljas/Min-1.pdf
https://www.pmf.unizg.hr/_download/repository/uvod_mineralogija.pdf
3.2. Sedam
kristalnih sustava
Njemački
mineralog Christian Samuel Weiss (1780. – 1856.) istraživao je oblik i simetriju
velikog broja kristala različitih
minerala. Na temelju elemenata makrosimetrije kristala (ravnine, osi,
centar
simetrije) te kutova među plohama i bridovima, došao je 1813. godine do
zaključka da se svi kristali mogu svrstati u šest kristalnih sustava
ili
singonija. Kristalne sustave definirao je koordinatnim sustavom s trima
osima koje
se pod jednakim ili različitim kutovima sijeku u jednoj točki u
središtu
kristala. Kristali trigonske simetrije, koje su tada svrstavali u
heksagonski sustav,
od sredine 20. stoljeća svrstavaju se u poseban trigonski sustav. Zato
danas
govorimo o sedam kristalnih sustava.
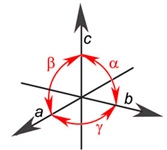
Slika 3.9.
Osni križ. Svi se kristali
mogu svrstati u sedam kristalnih sustava definiranih koordinatnim
sustavom s
trima osima uzduž kojih su periodičnosti a, b, c
te kutovi među
među osima α,
β, γ.
Tablica 3.1. Kristalni sustavi
|
Kristalni sustav |
Periodičnosti |
Kutovi |
Simetrijski elementi |
|
Kubni |
a = b = c |
α = β = γ = 90o |
3
osi četvrtoga reda |
|
Tetragonski |
a = b ≠ c |
α = β = γ = 90o |
1 os četvrtoga reda |
|
Rompski |
a ≠ b ≠ c |
α = β = γ = 90o |
3
osi drugoga reda ili 2
simetrijske ravnine |
|
Heksagonski |
a = b ≠ c |
α = β = 90o γ =
120o |
1 os šestoga reda |
|
Trigonski |
a = b ≠ c a = b = c |
α = β = 90o γ = 120o α = β = γ ≠ 90o |
1 os trećega reda |
|
Monoklinski |
a ≠ b ≠ c |
α = γ =
90o β ≠ 90o |
1 os drugoga reda ili |
|
Triklinski |
a ≠ b ≠ c |
α≠ β ≠ γ ≠ 90o |
nema |
Doznajte više na: https://en.wikipedia.org/wiki/Crystal_system
3.3. Označavanje
ploha na kristalu
Karakteristično
svojstvo
svake plohe na kristalu jest njezin položaj u odnosu na kristalografske
osi. Orijentacija
plohe u prostoru jednoznačno je određena odsječcima na kojima ploha
siječe
kristalografske osi a, b i c. Položaj pojedinih ploha u odnosu na
kristalografske osi odredi se tako da se jedna ploha, koja siječe sve
tri osi,
odabere za osnovnu ili jediničnu plohu. Za jediničnu
plohu uzima se da sve tri osi siječe na jediničnim
udaljenostima pa su
Weissovi parametri za tu plohu 1a : 1b : 1c.
Parametri (odsječci) jedinične plohe služe kao jedinica mjere za ostale
plohe
na kristalu. Parametri ostalih ploha, ma
: nb : pc, višekratnici su parametara (odsječaka) osnovne
plohe.
Koeficijenti m, n, i p
cijeli su brojevi ili jednostavni
razlomci. Takav način označavanja položaja ploha na kristalu uveo je
1817.
godine njemački kristalograf Christian Samuel
Weiss (1780. -
1856). Weissovi
parametri pokazuju koliko je puta odsječak neke plohe veći ili manji od
odsječka
jedinične plohe na toj istoj osi.
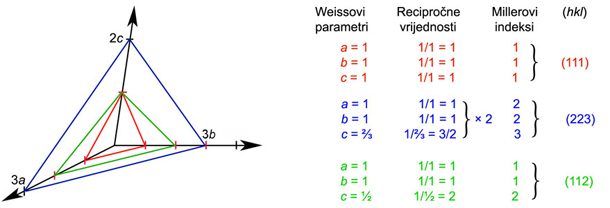
Slika
3.10. Weissovi parametri. Crveno označena ploha siječe osi na
jediničnim
odsječcima pa su Weissovi parametri jedinične plohe 1a :1b :1c. Plavo
označena
ploha siječe os a na 3a, os b na 3b i os c na 2c, pa se odsječci odnose
kao 3a
: 3b : 2c. Podijelimo ovaj odnos s 3, da bismo dobili jedinične
odsječke, pa za
tu plohu dobivamo Weissove parametre a : b : ⅔c.
Zeleno označena ploha siječe os a na 2a, os b na 2b, os c na 1c, pa se
odsječci
odnose kao 2a : 2b : c. Podijelimo ovaj odnos s 2, pa dobivamo Weisove
parametre a : b : ½c.
Na
temelju promatranja i
mjerenja položaja ploha na kristalima proizašao je i zakon
o racionalnom odnosu parametara: Na kristalu su moguće samo
one plohe čiji osni odnosi u usporedbi s osnim odnosom jedinične plohe
daju
male cijele brojeve ili jednostavne razlomke (René-Just Haüy, 1784., 1801.).
3.4.
Millerovi indeksi kristalnih ploha
Zapis
Weissovih parametara
relativno je složen. Engleski mineralog W.H. Miller
(1801. – 1880.) predložio je 1839. godine
da se kristalne plohe obilježavaju recipročnim vrijednostima Weissovih
parametara.
Odnos među Weissovim parametrima i Millerovim indeksima vidljiv je iz
opisa na
slici 3.10. Millerovi indeksi pišu se u okruglim zagradama tako da se
na prvom
mjestu nalazi indeks za os a, na
drugom za os b i na trećem za os c. Ako ploha siječe neku os u negativnom
dijelu koordinatnog sustava, tad se iznad indeksa dotične plohe stavlja
znak
minus, kao što je pokazano na slici 3.11.
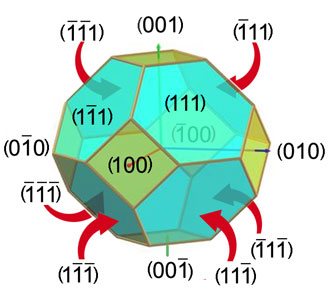
Slika 3.11.
Na slici 3.1. prikazan je
kristal fluorita, odnosno kalcijeva fluorida, CaF2. Kristalizira u kubnom sustavu,
najčešće u formi oktaedra i kocke. No, česte su i kombinacije obje
forme.
Tijelo koje sadržava plohe kocke i oktaedra naziva se kubooktaedar. Na
ovoj su
slici prikazani Millerovi indeksi svih ploha kubooktaedra.
Upamtite:
Kad je
Millerov indeks nula, ravnina
je paralelna s tom osi.
Kad je
Millerov indeks manji,
ravnina i pripadna os zatvaraju manji kut.
Kad je Millerov indeks veći, ravnina je sve bliže okomici na tu os.
Orijentacija ravnine u odnosu na kristalografske osi ne mijenja se ako
Millerove indekse pomnožimo nekim brojem. Primjerice ravnine s
indeksima (110),
(220), (330), (440) međusobno su paralelne.
3.5.
Kristalne forme
Kristalna
forma je skup simetrijski identičnih ploha, odnosno ploha
koje su međusobno povezane simetrijskim elementima. Sve plohe neke
forme imaju
isti odnos prema simetrijskim elementima. Primjerice, prirodni
nebrušeni
dijamant, prikazan na slici 3.12., ima formu oktaedra. Pojedinačne
plohe
oktaedra označuju se Millerovim indeksima u okruglim zagradama.
Primjerice, u kubnom
sustavu indeks (111) označuje samo onu plohu oktaedra koja osi siječe
na
jediničnim udaljenostima. Oktaedarska forma označuje se indeksom bilo
koje
njezine plohe, ali u vitičastoj zagradi. Primjerice, {111} označuje
oktaedar
kao formu, {100} označuje kocku kao formu, a {110} označuje rompski
dodekaedar.
Plohe rompskog dodekaedra sijeku dvije osi na jediničnim udaljenostima,
a s
trećom su osi paralelne. Razlikujemo zatvorene i otvorene kristalne
forme.
Zatvorena
forma, kao što je
oktaedar, heksaedar ili rompski
dodekaedar, u
potpunosti
zatvara cijeli prostor kristala. Na istom se kristalu može kombinirati
više
formi. Primjerice, kubooktaedar (slike 3.1. i 3.11.) je kombinacija
kocke i
oktaedra.

Slika 3.12. a) Prirodni nebrušeni dijamant (4,37 karata, 9,5×8×7 mm3, cijena 7690 $ + troškovi dostave), b) Oktaedar. Ucrtajte osni križ na oktaedru i upišite Millerove indekse svih ploha služeći se slikom 3.11. kao predloškom.
Otvorena
forma je ona koja ne
zatvara cijeli prostor kristala pa je nužna
kombinacija više formi. Na kristalu berila, prikazanom na slici 3.5.,
vidi se
kombinacija dviju formi; heksagonske prizme i pinakoida. Ni heksagonska
prizma,
niti pinakoid, ne mogu u cijelosti zatvoriti prostor kristala. Pinakoid je kristalna forma koja se sastoji
od dviju paralelnih ploha.
Zadatak:
Izradite papirnate modele tetraedra, oktaedra, kocke i kubooktaedra te
na njima
uočite simetrijske elemente: ravnine, osi i centar simetrije. Tako ćete
se
zabaviti, razviti motoriku prstiju i usput nešto naučiti.
Odgovarajuće
upute možete naći na YouTube-u, primjerice:
https://www.youtube.com/watch?v=phhVl-N9M4Y
https://www.youtube.com/watch?v=i5QtqYWS5-I
3.6.
Kristalni razredi ili kristalne klase
Njemački
liječnik Johann Friedrich Christian Hessel
(1796. – 1872.)
1830. godine prvi je dokazao da kristali mogu imati samo simetrijske
osi drugoga,
trećega, četvrtoga i šestoga reda. Uzimajući u obzir moguće kombinacije
simetrijskih
elemenata kristala (ravnine, centar simetrije, osi i složene
simetrijske
elemente koji uključuju rotaciju i inverziju) pokazao je da se svi
kristali
mogu svrstati u 32 kristalna razreda ili kristalne klase. U svakoj
kristalnoj
klasi moguće je sedam različitih kristalnih formi zbog toga što plohe
mogu
zauzimati sedam različitih položaja u odnosu na kristalografske osi,
što se
može prikazati sa sedam različitih tipova Millerovih indeksa. No, to su
već
sadržaji za veliku školu kristalografije i pitanja za studente
mineralogije.
4. Unutarnja građa
kristala
Kristal
je uvijek omeđen
plohama. O položaju ploha na kristalu ovisi njegov oblik. Postavlja se
pitanje
je li položaj ploha na kristalu slučajan ili se pokorava određenim
pravilima.
Francuski mineralog, opat René
Just Haüy, već je 1781. godine došao na
misao da pravilne geometrijske oblike kristala objasni njihovom
unutarnjom
građom. Zamišljao je da su kristali građeni od vrlo malih čestica,
molekula
sastavljačica, kojima je pripisao formu paralelopipeda. Slažući
paralelopipede
poput cigala mogao je izgraditi bilo koju pravilnu geometrijsku formu
kristala.
Haüyeva teorija, kao ideja, dala je bitan doprinos razvoju
kristalografije.
Godine 1813. engleski kemičar i fizičar William Hyde Wollaston
(1766. –
1828.) predložio je da se Haüyeve poliedarske molekule zamijene
kuglicama,
odnosno matematičkim točkama. Na osnovi toga stvorena je predodžba o
unutarnjoj
građi kristala kao uređenom trodimenzijskom razmještaju istovrsnih
čestica,
atoma, iona ili molekula. Istovrsne čestice u kristalu leže na
pravcima, uvijek
na jednakoj udaljenosti jedna od druge, kao što je prikazano na slici
4.1.
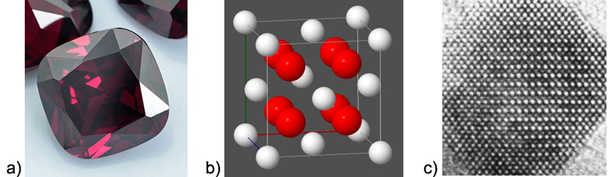
Slika 4.1. a) Sintetički dobiveni kubni kristali cirkonijeva dioksida bezbojni su. Dodatkom tragova kobalta, titanija, cerija i kroma mogu se dobiti crveni, zeleni, žuti i narančasti kristali. Rabe se kao nakit zbog velikog indeksa loma svjetlosti i tvrdoće 8 – 8,5 na Mohsovoj ljestvici. b) Ioni cirkonija i kisika u kristalu leže na pravcima uvijek na jednakoj udaljenosti jedni od drugih. c) Uređeni razmještaj cirkonijevih i kisikovih iona u kristalu cirkonijeva dioksida vidi se pomoću elektronskoga mikroskopa. (Snimila prof.dr.sc. Anđelka Tonejc, profesor Fizičkog odsjeka PMF-a Sveučilišta u Zagrebu.)
4.1.
Kristalna rešetka
Sigurno
ste imali priliku vidjeti različite vrpce ili trake na kojima
su izvezeni ili otisnuti neki motivi. Ako ste bolje pogledali, mogli
ste uočiti
da se na vrpci isti motiv periodički ponavlja svakih nekoliko mm ili
cm. Da
biste shvatili izgled cijele vrpce dovoljno je proučiti samo osnovni
motiv koji
se periodički ponavlja uzduž vrpce odnosno pravca.

Slika 4.2.
Dio
oltarne pregrade iz 11. stoljeća (Arheološki muzej Zadar). Translacijom za duljinu a uzduž translacijske
osi uvijek se iz bilo koje točke na ovom pleteru dolazi u istovrsnu
točku.
Izvor: R. Ivančević, Umjetničko blago Hrvatske, Jugoslavenska revija
Beograd i
IRO Motovun, 1986.
Na
dekoriranom platnu ili papiru,
ili na podu od keramičkih pločica, možete uočiti postojanje dvaju
smjerova u
kojima se isti motiv nakon određene udaljenosti periodički ponavlja.
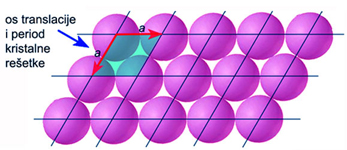
Slika 4.3. U sloju najgušće složenih jednakih kuglica (atoma) možemo uočiti dva smjera u kojima se isti razmještaj kuglica periodički ponavlja. Zakonitost periodičnog ponavljanja unutar sloja nazivamo dvodimenzijskom kristalnom rešetkom. Smjer periodičnog ponavljanja istog razmještaja kuglica naziva se translacijska os ili os kristalne rešetke. Udaljenost nakon koje se dolazi u istu točku ili čvor kristalne rešetke naziva se period kristalne rešetke. U sloju gusto složenih jednakih kuglica imamo dvije jednake translacijske osi a, pod kutom od 120o.
Kristali
su trodimenzijske
tvorevine pa se u njima isti razmještaj atoma, iona ili molekula
periodično
ponavlja u tri smjera u prostoru. Zakonitost toga periodičnog
ponavljanja
opisuje se kristalnom rešetkom. Kristalna
rešetka je zamišljena beskonačna tvorevina u kojoj se
polazeći iz bilo koje
točke u istovrsnu točku u prostoru može doći translacijom (lat. translatio - prijenos) uzduž određenih
smjerova. Da bismo jednoznačno definirali rešetku moramo znati smjer u
kojem se
istovrsni razmještaj periodički ponavlja i udaljenost na kojoj se u tom
smjeru
dolazi u istovrsnu točku. Taj smjer zove se translacijska
os ili os
kristalne rešetke, a duljina periodičkog ponavljanja je period kristalne
rešetke. Već smo kazali da su kristali trodimenzijske
tvorevine, zato moramo naći tri smjera u kojima se istovrsni razmještaj
točaka
(atoma, iona, molekula) periodički ponavlja u prostoru. Tri
translacijska
smjera u prostoru, odnosno tri osi kristalne rešetke, kao i njihove
periode, označujemo
slovima a, b, c, a kutove što ih
osi
međusobno zatvaraju grčkim slovima alfa (a),
beta (b) i
gama (g).
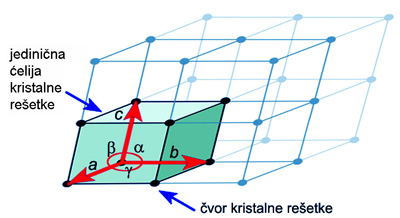
Slika 4.4.
Shematski
prikaz jedinične ćelije kristalne rešetke. Jedinična ćelija je najmanji
dio
kristalne rešetke koji se periodički ponavlja u tri smjera u prostoru.
Svaka
kristalizirana tvar ima samo njojzi svojstvenu jediničnu ćeliju
kristalne
rešetke definiranih duljina osi i kutova što ih osi međusobno zatvaraju.
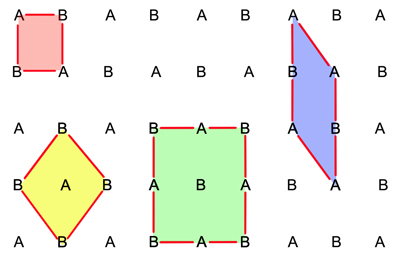
Slika 4.5.
Izbor jedinične ćelije
kristalne rešetke.
Jediničnu ćeliju kristalne rešetke ne može se odabrati bilo kako već se treba pridržavati pravila koje je još 1848. g. našao A. Bravais, a to je da volumen jedinične ćelije mora biti minimalan, broj pravih kutova maksimalan te da simetrija rešetke mora biti jednaka simetriji kristala. Slika 4.5 na zoran način obrazlaže ta pravila na primjeru dvodimenzijske kristalne rešetke. Ružičasto obilježena ćelija ne udovoljava osnovnom pravilu, a to je da se translacijom iz točke A opet mora doći u točku A. Ćelije obilježene žutom i plavom bojom zadovoljavaju uvjet najmanjeg volumena. No, pravi izbor je ćelija obilježena zelenom bojom. Iako ta ćelija ima veći volumen ona ispunjava i uvjet maksimalnog broja pravih kutova.
4.2. Bravaisove
prostorne rešetke
Francuski
fizičar i mineralog
Auguste Bravais
(1811.
–
1863.) 1848. g. matematički je opisao sve moguće
trodimenzijske prostorne rešetke. Prvi je došao do zaključka da je u 7
kristalografskih sustava moguće načiniti samo 14 različitih prostornih
rešetki
uz uvjet maksimalnog broja pravih kutova i najmanji volumen
ćelije/ciglice. Tih
14 rešetki, prikazanih na slici 4.6., danas nazivamo Bravaisove
prostorne
rešetke. Svi čvorovi pojedine Bravaisove rešetke potpuno su
ekvivalentni, odnosno
imaju potpuno isto prostorno okruženje. U bilo kojoj realnoj kristalnoj
strukturi razmještaj atoma, iona ili molekula u sva tri smjera u
prostoru
periodički se ponavlja po zakonitosti samo jedne od Bravaisovih
rešetki.
Primjerice, a-polonij
kristalizira tako da atomi polonija zauzimaju vrhove kocke. Bravaisova
rešetka
kristalne strukture a-polonija
je primitivna kubna s bridom
jedinične
ćelije a = 335 pm. Atomi polonija
na
vrhovima kocke istodobno pripadaju k osam jediničnih ćelija. Kako kocka
ima 8 vrhova
a svaki atom na vrhu pripada samo ⅛ pojedinoj jediničnoj ćeliji, proizlazi
da jedinična ćelija a-polonija
sadržava samo 1 atom. Općenito, sve
primitivne (P) jedinične ćelije Bravaisove rešetke sadržavaju jedan
čvor. Sve jedinične
ćelije prostorno centrirane (I) i bazno centrirane rešetke (A, B ili C)
sadržavaju dva čvora. Sve jedinične ćelije plošno centrirane rešetke
(F) sadržavaju
četiri čvora kao što je vidljivo iz slike 4.6. Oznaka P
dolazi od eng. primitive,
oznaka I od njem.
innenzentriertes,
oznaka F
od
engl. face. Oznake A,
B
ili C ovise o orijentaciji rešetke,
odnosno koja je ploha uzeta za bazu. Uobičajeno je da to bude C, odnosno ploha koja siječe os c.
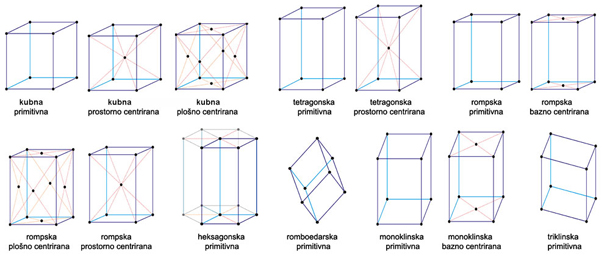
Slika 4.6.
Bravaisove prostorne rešetke
4.3. Prostorne grupe
simetrije
Tijekom
druge polovine 19. stoljeća razvijaju se teorije o unutarnjoj
simetriji i uređenosti kristalnih struktura. Bilo je očito da
simetrijske
operacije ne određuju samo vanjski izgled kristala nego i razmještaj
atoma u
kristalnoj strukturi. Osim simetrijskih elemenata prisutnih na
kristalnim
poliedrima, do periodičnog ponavljanja razmještaja atoma u kristalnoj
strukturi
dovode i simetrijski elementi koji uključuju translaciju, vijčane ili
helikoidalne osi te klizne simetrijske ravnine.
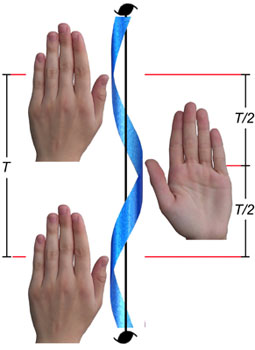
Slika 4.7. Simetrijska operacija vijčane ili helikoidalne osi sastoji se od zakreta za kut 2p/n (n = 2, 3, 4, 6) i pomaka duž translacijske osi za T/2, T/3, T/4, odnosno T/6. Na slici je prikazana operacija helikoidalne osi drugoga reda što uključuje zakret za 180o u smjeru suprotnom od smjera kretanja kazaljke na satu i pomak za pola perioda kristalne rešetke prema gore. Pri operaciji vijčane osi molekula ostaje nepromijenjena. Nakon rotacije za 180o i translacije za T/2 vidimo dlan umjesto gornje strane ruke kao što je prikazano na slici.
U
kristalnim strukturama helikoidalne osi mogu ići jedino duž smjerova
paralelnih s običnim osima na kristalima. Helikoidalne osi mogu biti
lijeve ili
desne. Ako je os vertikalna, pod lijevom osi razumijeva se zakretanje u
smjeru
suprotnom od smjera kretanja kazaljke na satu i pomak prema gore. Za
helikoidalnu os drugoga reda svejedno je jeli zakret ulijevo ili
udesno, ali ne
i za osi trećega, četvrtoga i šestoga reda.
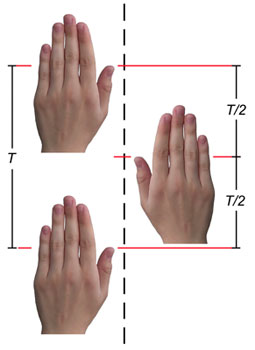
Slika 4.8.
Simetrijska
operacija klizne simetrijske ravnine sastoji se od zrcaljenja i
klizanja
paralelno s tom ravninom za pola perioda a, b, ili c, ovisno uzduž koje
se osi
događa klizanje. Pritom se originalna i zrcalno simetrična molekula
odnose kao
lijeva i desna ruka. Pod dijagonalno ili n klizanje razumijeva se
klizanje za
pola perioda uzduž dijagonale između dviju osi. Oznaka d odnosi se na
dijagonalno klizanje za ¼ perioda. Doznajte više na:
https://www.pmf.unizg.hr/_download/repository/Min-2%5B4%5D.pdf
http://www.phy.pmf.unizg.hr/~atonejc/2%20Osnove%20kristalne%20struktureNANO.pdf
Kraj 19.
stoljeća uzbudljivo je razdoblje kristalografije.
Pretpostavlja se uređeni razmještaj atoma u kristalu. Kombinacijom 14
Bravaisovih rešetki i 32 kristalne klase simetrije te uvođenjem
dodatnih simetrijskih
operacija, vijčanih (helikoidalnih) osi i kliznih ravnina, dolazi se do
230 prostornih grupa, odnosno
načina na koji se neka točka (atom, ion ili molekula) može periodički
ponavljati u prostoru. Prostorne grupe su od 1890. do 1894. godine
neovisno
otkrili ruski kristalograf Jevgraf S. Fjodorov
(1853. – 1919.)
i njemački matematičar Arthur M. Schoenflies
(1853. – 1928.).
Tu se spominje i engleski geolog i kristalograf William Barlow
(1845. – 1934.)
koji je neovisno došao do otkrića 230 prostornih grupa, ali je to
prekasno
objavio, 1894.
Značaj Fjodorovog otkrića može se ilustrirati činjenicom da su sve kristalne strukture istražene do 1980-ih mogu uklopiti u jednu od 230 prostornih grupa. Tek su 1982. godine nađene kristalne strukture, tzv. kvazikristali, koji se nisu mogli uklopiti niti u jednu od klasičnih prostornih grupa simetrije. O kvazikristalima doznajte više na adresi: https://hrcak.srce.hr/83947
4.4. Slagaline kuglica
jednake veličine
Na osnovi
spoznaja o
simetriji i kemijskom sastavu kristala znanstvenici su još u 19.
stoljeću pretpostavili
neke jednostavnije kristalne strukture. Dobar primjer je niz kristalnih
struktura koje je 1883. objavio engleski geolog i kristalograf William
Barlow.
Atome je smatrao čvrstim kuglicama. Tako je za kristale koji se sastoje
samo od
jedne vrste atoma predvidio strukture najbliže gustoj slagalini kuglica
jednake
veličine. Razmatrajući moguće slaganje kuglica različitih veličina
točno je
predvidio strukture slične strukturama NaCl i CsCl (Slika 4.9.)
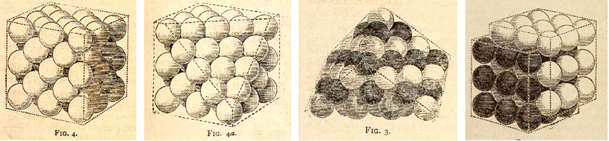
Slika 4.9. W. Barlow,
Probable Nature of the Internal Symmetry of Crystals, Nature, 1883, 29,
186-188.
Izvor:
https://www.nature.com/articles/029186a0.pdf
U ovom
ćemo se poglavlju malo
zabaviti slaganjem kuglica jednake veličine i prazninama koje pritom
nastaju.
Ta su nam znanja važna za bolje razumijevanje nekih jednostavnijih
kristalnih
struktura metala i ionskih spojeva. Naime, većinu kristalnih struktura
određuje
načelo najgušćeg slaganja. Kako su anioni uvijek veći od kationa, mnoge
se
ionske strukture mogu opisati kao guste slagaline aniona, i kationa
koji
popunjavaju praznine među anionima. Krajem 19. i početkom 20. stoljeća
kristalne strukture minerala, metala i najjednostavnijih kemijskih
spojeva, kao
što je natrijev ili cezijev klorid, bile su potpuna nepoznanica. Ipak,
u ovom
poglavlju koristit ćemo i suvremena znanja o kristalnim strukturama
nekih
metala i ionskih spojeva. O tome kako su otkrivene njihove strukture
bit će
riječi u poglavlju 5. X-zrake.
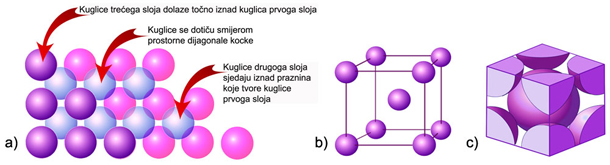
4.4.1. Primitivna (jednostavna) kubna rešetka
Jedinična
ćelija bilo koje
primitivne kristalne rešetke sadržava samo jedan čvor. To je najmanja
moguća
ćelija. Već smo kazali da a-polonij
kristalizira po tipu primitivne kubne Bravaisove
rešetke s bridom jedinične ćelije a
=
335 pm.
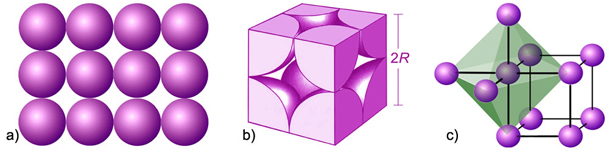
Slika 4.10. a) Način slaganja atoma u primitivnoj (jednostavnoj) kubnoj rešetki. Atomi narednog sloja dolaze točno iznad atoma prethodnog sloja. b) Jedinična ćelija a-polonija sadržava samo 1 atom. c) Svaki je atom oktaedarski okružen sa šest atoma na jednakoj udaljenosti.
Kubna
primitivna rešetka nije
primjer guste slagaline. Naprotiv, popunjenost prostora vrlo je mala, a
izračunat ćemo je tako da volumen kugle radijusa R
= a/2 podijelimo
volumenom kocke, V = a3.

U
središtu primitivne kubne rešetke
ostala je velika praznina koju mogu popuniti manji atomi ili ioni.
Kristalne
strukture cezijeva klorida (a = 411,9 nm), bromida (a = 429,1
pm) i jodida
(a = 450,3
pm) lijep su primjer ionske strukture u kojoj manji kation ulazi
u šupljinu koju tvore veliki anioni. Takvim
načinom slaganja postiže se najmanja energija kristala. U strukturama
CsCl, CsBr i CsI koordinacijski broj kationa i aniona jednak je 8. Pazite! Kristalne rešetke cezijeva
klorida, bromida i jodida su primitivne, a ne prostorno centrirane, kao
što se
to često misli ili može naći na Internetu. Kloridni ioni čine jednu
primitivnu
rešetku, a cezijevi ioni drugu primitivnu rešetku. Te su rešetke
međusobno
pomaknute za polovinu duljine brida jedinične ćelije u sva tri smjera u
prostoru. Uzmemo li ion klora kao ishodište koordinatnog sustava, tad
su
njegove koordinate u kristalnoj rešetki: x,y,z
= 0,0,0. Ion cezija nalazi se u središtu primitivne rešetke što je čine
ioni
klora pa su koordinate cezijeva iona: x,y,z
= ½,½,½.

Slika 4.11.
a) Kristalna struktura
cezijeva klorida, bromida i jodida. Svaki je ion cezija okružen s osam
iona
klora i obratno. Broj atoma ili iona koji okružuje neki atom ili ion
naziva se koordinacijskim brojem, (KB).
U ionskim
strukturama uvijek kation stavljamo u središte koordinacijskog poliedra
čiji su
bridovi linije koje spajaju središta aniona. U koordinacijski poliedar
kationa
ulaze samo oni anioni koji ga dodiruju. b) Jedinična ćelija cezijeva
klorida,
bromida i jodida sadržava jednu formulsku jedinku CsX. c) Koordinate
iona Cl‒ i Cs+ u kristalnoj rešetki
cezijeva klorida.
Strukturu
tipa CsCl imaju
ionski spojevi s velikim kationom, primjerice amonijev klorid. Po
strukturnom
tipu cezijeva klorida kristaliziraju: b-mjed
(CuZn), AgZn, BeCu, AlNi, AgMg i drugi međumetalni (intermetalni)
spojevi.
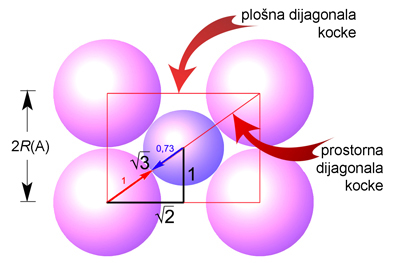
Slika 4.12.
Lako je izračunati omjer radijusa
velikog aniona, R(A), prema radijusu manjeg kationa, r(K), koji ulazi u
prazninu
u središtu primitivne kubne slagaline kuglica jednake veličine. To
znači da
se kation i anion
dotiču smjerom prostorne
dijagonale kocke. Ako je brid kocke a = 2R(A), tad je razmak između
aniona i
kationa, R(A) + r(K), jednak polovini dijagonale kocke. Kao što se vidi
sa
slike proizlazi da je omjer radijusa aniona i kationa, R(A) : r(K) = 1
: 0,73.
Ako je brid jedinične ćelije cezijeva jodida, a = 450,3 pm, i pretpostavimo da se jodidni ioni dotiču, tad je radius jodidnog iona,
R(l-) = a/2 = 450,3 pm/2 = 225,1 pm.
Za prostornu dijagonalu jedinične ćelije dobivamo:
dćelije= a × √3 = 450,3 pm × √3 = 780 pm.
Zbroj radijusa iona I‒ i Cs+ jednak je polovini prostorne dijagonale jedinične ćelije, odnosno 390 pm. Oduzmemo li od ove vrijednosti radijus jodidnog iona, za radijus iona cezija dobivamo:
r(Cs+) = 390 pm - 225 pm = 165 pm.
Odavde proizlazi da je omjer
R(I‒) : r(Cs+) = 225 pm : 165 pm = 1 : 0,73,
a to je
upravo idealan omjer radijusa,
kao što se
vidi iz opisa slike 4.12. U različitim tablicama ionskih radijusa
najčešće se nalaze
ove vrijednosti: r(I‒)
= 220
pm, r(Br‒)
= 191
pm, r(Cl‒)
= 181 pm i r(Cs+)
= 167 pm. To su srednje vrijednosti ionskih radijusa dobivene sličnim
postupkom
iz podataka za veći broj kristalnih struktura. Naš se rezultat dobro
slaže s
vrijednošću iz tablica. Općenito, atomski i ionski radijusi su donekle
promjenjive veličine jer ovise o broju i vrsti iona, molekula ili atoma
koji ih
okružuju. Atomi, ioni i molekule nisu tvrde kuglice.
4.4.2. Prostorno
centrirana kubna rešetka
Prostorno
centrirana kubna
rešetka (BCC - Body Centred Cubic
Lattice)
sadržava dva istovrsna čvora,
na vrhovima
i u središtu kocke. Drugim riječima, istovrsni atomi zaposjedaju vrhove
i
središte kocke.
Slika 4.13.
a) Način slaganja kuglica (atoma) u BCC rešetki pokazuje da u njoj nema
gusto
složenih slojeva kuglica (atoma). b) U BCC rešetki KB = 8, jer je svaki
atom okružen
s osam jednakih atoma na jednakoj udaljenosti. c) Jedinična ćelija BCC
rešetke
sadržava dva čvora (atoma).
Ni kubna prostorno
centrirana rešetka nije primjer najgušće slagaline. Popunjenost
prostora
izračunat ćemo na već uobičajeni način tako da volumen dviju kuglica,
koje se
dotiču smjerom prostorne dijagonale, podijelimo volumenom kocke.

Mnogi
metali, primjerice; Li,
Na, K, Rb, Cs, V, Cr, a-Fe,
Ba, Nb, Mo, Ta i W kristaliziraju po tipu kubne prostorno centrirane
rešetke.
Dok su alkalijski metali mekani, prijelazni metali s BCC strukturom
općenito su
tvrđi i manje plastični u odnosu na metale kao što su Cu, Au i Ag s FCC
strukturom (FCC - Face Centered Cubic Lattice).
To je posljedica različite elektronske konfiguracije atoma alkalijskih
metala i
prijelaznih metala. Naime, kod prijelaznih metala i d-elektroni
sudjeluju u stvaranju metalne veze.
U
prostorno centriranoj kubnoj rešetki mogu se uočiti deformirane
oktaedarske
i tetraedarske praznine. Iako su deformirane, ove su praznine neobično
važne za
strukturu i svojstva čelika.
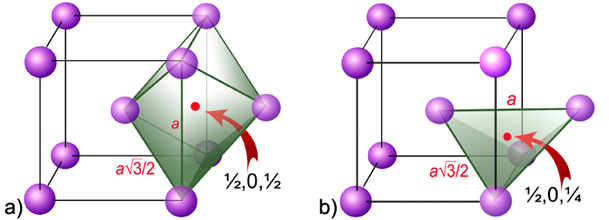
Slika 4.14. a) Crvena točka na slici označuje jednu oktaedarsku prazninu u BCC rešetki na koordinati ½,0,½. Takvih praznina u jediničnoj ćeliji BCC rešetke ima šest i to na središtima ploha i na raspolovnicama bridova (6×½ + 12×¼ = 6). b) Prikazana tetraedarska praznina u BCC rešetki nalazi se na koordinati ½,0,¼. Na svakoj plohi nalaze se četiri takve praznine, pa jedinična ćelija BCC rešetke sadržava 12 tetraedarskih praznina (6 × 4 × ½ = 12).
Omjer
radijusa atoma koji se dotiču smjerom prostorne dijagonale u BCC
rešetki i radijusa oktaedarske praznine može se izračunati pomoću
Pitagorina
poučka, pa se dobiva: R(atom) : r(okt. pr.) = 1 : 0,155. Jednakim
postupkom za omjer radijusa atoma i tetraedarske praznine u BCC rešetki
dobiva
se da je:
R(atom) : r(tetr.
pr.) = 1 : 0,29.
Pri
temperaturi nižoj od 912 oC željezo
kristalizira po
tipu BCC rešetke. Za radijus atoma željeza, u tzv. alfa-željezu
ili feritu, uzima se R(a-Fe)
= 126
pm. Odavde proizlazi da radijus oktaedarske praznine u a-Fe
iznosi:
R(a-Fe) : r(okt.
pr.) = 1 : 0,155 = 126 pm : 19,5
pm.
Za
radijus tetraedarske praznine dobivamo:
R(a-Fe) : r(tetr.
pr.) = 1 : 0,29 = 126 pm : 36,5
pm.
Ugljik,
kojeg željezo uvijek sadržava, najbolji je kandidat za
popunjavanje oktaedarskih i tetraedarskih praznina u željezu. Radijus
ugljika
je r(C) = 77 pm, što je znatno više
od radijusa tetraedarske i oktaedarske praznine. Zato je topljivost
ugljika u alfa-željezu vrlo mala.
Kad se površina
običnog, tzv. mekanog željeza izbrusi, nagrize kiselinama i pogleda pod
metalografskim mikroskopom, vide se svijetla kristalna zrna alfa-željeza (ferit), a na granicama zrna
crne kuglice ili lamele od ugljika (grafit).
4.4.3.
Plošno centrirana kubna rešetka
Plošno
centrirana kubna rešetka (FCC - Face Centred Cubic Lattice) sadržava 4
istovrsna
čvora i to na vrhovima i središtima ploha kocke, kao što se vidi sa
slike 4.15.
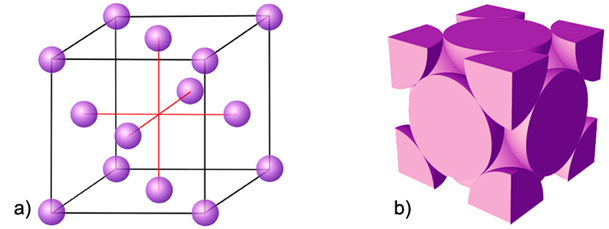
Slika
4.15. a)
Razmještaj čvorova (atoma) u kubnoj plošno centriranoj rešetki. b)
Čvorove
(atome) na vrhovima dijeli osam susjednih jediničnih ćelija, pa oni
samo jednom
osminom pripadaju istoj jediničnoj ćeliji. Čvorove na središtima ploha
dijele
dvije susjedne jedinične ćelije, pa oni samo jednom polovinom pripadaju istoj jediničnoj ćeliji.
FCC rešetka sadržava 4 čvora (8 × ⅛
+ 6 × ½ = 4).
Po tipu
plošno centrirane rešetke kristaliziraju mnogi tehnički važni
metali, primjerice; Al, Ca, Sr, Ni, Cu, Rh, Pd, Ag, Ir, Pt, Au, Pb i gama-Fe. U kristalnim rešetkama
nabrojenih
metala KB = 12, jer je svaki atom okružen s 12 jednakih atoma na
jednakoj
udaljenosti.

Slika 4.16. Kubooktaedar je koordinacijski poliedar u kristalnim strukturama metala s FCC rešetkom.
Kubna
plošno centrirana rešetka, FCC, i heksagonska gusta slagalina,
HCP (Hexagonal Close Packed)
najgušće su moguće slagaline kuglica jednake veličine. Uočite da se u
plošno
centriranoj kocki kuglice dotiču smjerom plošne dijagonale kocke, pa je
radijus
kuglice jednak četvrtini duljine njezine plošne dijagonale, odnosno R(atom) = a ×
√2/4.
Popunjenost
prostora izračunat ćemo na već uobičajeni način tako da volumen
četiriju
kuglica podijelimo volumenom kocke.
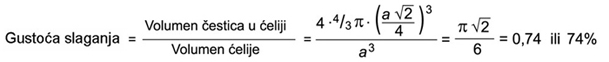
Najgušći
sloj kuglica u FCC rešetki podudara se s ravninom čiji su
Millerovi indeksi (111).
U tom najgušćem sloju
svaka je kuglica (atom) okružena sa šest kuglica na jednakoj
udaljenosti. Pogledamo
li malo detaljnije najgušći sloj kuglica (slika 4.17.), lako ćemo
uočiti da se
oko svake kuglice (atoma) unutar sloja nalazi šest trokutnih
praznina. Broj trokutnih
praznina u najgušćoj slagalini kuglica jednake veličine dvaput je veći
od broja
kuglica.
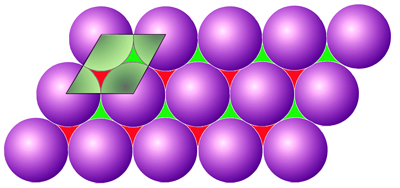
Slika 4.17. U najgušćim slagalinama slojevi se slažu jedan povrh drugoga tako da kuglice sljedećega sloja sjedaju u udubljenja koje čine tri kuglice prethodnoga sloja.
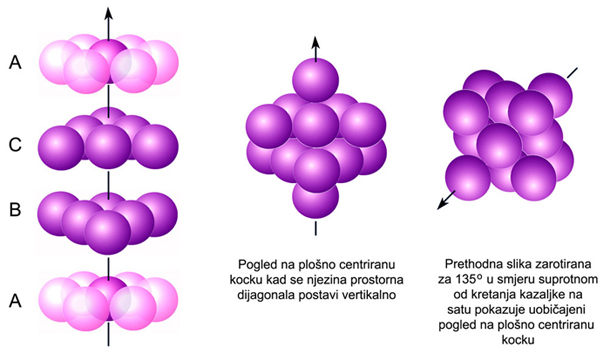
Slika 4.18. U kubnoj najgušćoj slagalini slojevi se slažu jedan iznad drugoga tako da kuglice sloja C dolaze iznad onih trokutnih praznina u sloju A koje nisu bile zauzete slojem B. (Vidi sliku 4.17.) Prema tome u FCC rešetki slojevi kuglica (atoma) slažu se redoslijedom ABCABC....
Već smo
kazali da jedinična ćelija FCC rešetke sadržava 4 atoma i da
na svaki atom dolaze dvije trokutne
praznine. No, osim trokutnih
praznina
jedinična ćelija FCC rešetke sadržava 8 tetraedarskih i 4 oktaedarske
praznine.
Tetraedarske praznine nalaze se na ¼,¼,¼
i na ekvivalentnim položajima u jediničnoj
ćeliji FCC rešetke.
Oktaedarske praznine nalaze se na ½,½,½ i ekvivalentnim
položajima, odnosno u središtu i na raspolovnicama bridova plošno
centrirane kocke.
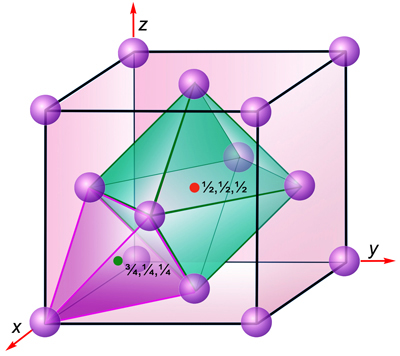
Slika
4.19. Tetraedarska i oktaedarska praznina u FCC rešetki
metala
Omjer radijusa atoma i praznina u FCC rešetki uz minimalno znanje geometrije lako je izračunati. Najbolje je crtati, prisjetiti se već stečenog znanja i računati. Središta tri atoma koji se međusobno dotiču čine jednakostranični trokut. Mali atom koji zauzima trokutnu prazninu nalazi se u težištu trokuta. Uzmemo li da je stranica trokuta a = 2, tad je njegova visina, v = √3, a to je ujedno i težišnica jednakostraničnog trokuta. Težište jednakostraničnog trokuta dijeli svaku težišnicu u omjeru 2:1. Uzmimo da je radijus velikog atoma R = 1, a radijus atoma u trokutnoj praznini r, tad je R + r = 2/3 × √3. Odavde se za omjer radijusa velikog atoma, R, prema radijusu malog atoma, r, u trokutnoj praznini dobiva:
R(atom) : r(trok.
pr.) = 1 : 0,155.
Sličnim
postupkom dobiva se da omjer radijusa velikog atoma, R,
i malog atoma, r, koji ulazi u
tetraedarsku prazninu FCC rešetke, iznosi:
R(atom) : r(tetr.pr.)
= 1 : 0,225.
Radijus
atoma koji ulazi u oktaedarsku prazninu najlakše je izračunati.
Četiri atoma čine kvadrat čija je dijagonala d
= 2R + 2r
= √2. Odavde se
dobiva sljedeći omjer radijusa:
R(atom) : r(okt.pr.)
= 1 : 0,414.
Vratimo
se opet željezu. U doba dok kristalne strukture željeza nisu
bile poznate promjene u "strukturi" metala mogle su se pratiti pomoću
krivulje
hlađenja ili pomoću
dilatometrijske krivulje. Dilatometrijska krivulja dobije
se tako da se prati promjena duljine uzorka u obliku štapa u ovisnosti
o njegovoj
temperaturi.
Kao što
sam naziv kaže, krivulja hlađenja pokazuje promjenu
temperature tijekom proteka vremena hlađenja, primjerice uzorka
rastaljena
željeza. Pri temperaturi 1538 oC dolazi do
kristalizacije (skrućivanja)
rastaljena željeza. Zbog oslobađanja topline kristalizacije temperatura
smjese
taline i kristala željeza ne mijenja se sve dok se svo željezo ne
skrutne
(kristalizira). Pritom željezo kristalizira po tipu BCC rešetke.
Željezo s BCC rešetkom
pri toj visokoj temperaturi naziva se delta-željezo.
Tijekom hlađenja delta-željeza
sljedeći zastoj temperature opaža se pri 1394 oC.
Pri toj
temperaturi dolazi do promjene kristalne strukture, odnosno BCC rešetka
mijenja
se u FCC rešetku. Željezo s takvom kristalnom strukturom naziva se gama-željezo. Daljnjim hlađenjem ponovo
dolazi do zastoja temperature pri 912 oC jer se
FCC rešetka željeza
promijeni u BCC rešetku. Ova se faza željeza naziva alfa-željezom
ili ferit. Daljnjim hlađenjem opet se opaža zastoj
pri temperaturi od 770 oC, ali kristalna
struktura se ne mijenja.
Pri toj temperaturi do tada paramagnetično željezo postaje
feromagnetično. Ova
temperatura naziva se Curieva točka. Na temelju rezultata dobivenih
krivuljom
hlađenja i dilatometrijom, željezo u temperaturnom području od 770 do
912 oC,
metalurzi su zvali beta-željezo, a
ono ispod 770 oC alfa-željezo.
No, nakon saznanja o kristalnim strukturama željeza, naziv beta-željezo postao je bespredmetan.
Već smo
kazali da je topljivost ugljika u alfa-željezu
vrlo mala, samo 0,025 % pri 723 oC. No, u gama-željezu, pri 1147 oC,
otapa
se čak 2,06 % ugljika. Kruta otopina ugljika u gama-željezu
naziva se austenit. No, obično željezo sadržava oko
0,8 % ugljika, a ono koje se rabi za specijalne alate sadržava oko 1,2
%
ugljika. Ugljik ulazi u oktaedarske praznine gama-željeza,
odnosno FCC rešetke. Već smo kazali da je u FCC
rešetki broj oktaedarskih praznina jednak broju atoma. To znači da je
samo dio
oktaedarskih praznina u FCC rešetki željeza zauzet atomima ugljika.
Pretpostavimo
da gama-željezo sadržava 1,2 %
ugljika. Udio zauzetih oktaedarskih praznina izračunat ćemo tako da
usporedimo količine
(množine) atoma željeza i ugljika.
n(Fe) : n(C) = (m(Fe)/M(Fe)
: (m(C)/M(C)
(98,8 g/55,85
g mol-1) : (1,2 g/12,0 g mol‒1)
1,77
: 0,1 = 1 : 0,056 = 100 : 5,6
U
navedenoj slitini željeza i ugljika samo je 5,6 % oktaedarskih
praznina zaposjednuto atomima ugljika. No, i ta tako mala količina
ugljika
određuje svojstva željeza. Ako se kruta otopina ugljika u gama-željezu (austenit) naglo ohladi s
oko 900 oC na
sobnu temperaturu, atomi ugljika ostaju na mjestu gdje su se zatekli,
ali se
kristalna rešetka željeza promijenila iz FCC u BCC. Taj se proces
naziva
kaljenje čelika. Pritom nastaje metastabilna faza koja se naziva
martenzit. Očito
je da atomi ugljika smetaju i uzrokuju deformacije i napetosti u BCC
rešetki. Zbog
toga se povećava unutarnje trenje i sprječava klizanje slojeva atoma,
pa
željezo postaje krhko poput stakla. Da je ova tvrdnja istinita lako se
možete
uvjeriti pokusom. Običnu ukosnicu užarite do crvenog usijanja i naglo
bacite u
hladnu vodu pa ćete je moći slomiti prstima.
(Pogledajte na Internetu: https://www.youtube.com/watch?v=cR9FX6-SI54).
Da bi se
postigla željena svojstva, kaljeni se čelik podvrgava
daljnjoj termičkoj obradi, primjerice zagrijavanju pri 200 do 400 oC.
Taj se proces naziva popuštanje. Pritom dolazi do smanjenja napetosti u
kristalnoj rešetki i migracije atoma ugljika. Pomoću metalografskoga
mikroskopa
na brušenim, poliranim i kiselinama nagrizanim uzorcima čelika
metalurzi će
prepoznati različite faze kao zaostali austenit, martenzit, perlit,
cementit
(Fe3C), ferit, grafit itd. Cementit, Fe3C,
ili željezov
karbid je kemijski spoj željeza i ugljika. To je krhak spoj s
kompliciranom
kristalnom strukturom, a nastaje kristalizacijom iz taline, ali se
izlučuje i u
krutini tijekom naknadne termičke obrade. Ovisno o uvjetima nastajanja
može
tvoriti odvojene pločaste kristale, lamele ili opne oko kristalnih
zrna. Ukratko,
termička obrada čelika i studij promjena koje se pritom događaju
posebna je znanost
kojom se bave metalurzi.
Promatrajući
modele BCC-rešetke i FCC-rešetke možda ste se upitali
kako se događaju te drastične promjene strukture i preslagivanje atoma
željeza.
Istraživanja su pokazala da fazna pretvorba
FCC
u BCC rešetku ne nastaje procesom difuzije već spada u veoma brze
nedifuzijske
procese. Možemo
zamisliti da se pri 912 oC FCC rešetka
komprimira smjerom [001]. Pritom dolazi do klizanja atoma željeza
smjerom [111], pa ti mali
pomaci dovode do promjene tipa kristalne rešetke čistoga željeza. No,
martenzit
koji nastaje naglim hlađenjem austenita ima tetragonsku prostorno
centriranu rešetku
(BCT - Body Centred Tetragonal),
vrlo blisku regularnoj BCC rešetki, ali neznatno većeg volumena.

Slika
4.20. Shematski
prikaz transformacije FCC u BCC rešetku. Crne točke označuju
oktaedarske
praznine koje su u ugljičnom čeliku djelomično zaposjednute atomima
ugljika. Pri
kaljenju čelika atomi ugljika ostaju
na svojim mjestima što uzrokuje deformacije i napetosti u BCC rešetki.
Zanimljivo je
izračunati i usporediti radijuse atoma u alfa
i gama-željezu. BCC rešetka željeza
ima brid a = 286,66 pm. Kako se u BCC rešetki atomi dotiču
smjerom prostorne dijagonale
kocke, za radijus atoma alfa-željeza
dobiva se:
R(a-Fe) = ¼
× a × √3 = ¼ × 286,66 pm ×
√3 = 124,13 pm.
U gama-željezu,
koje kristalizira po tipu
FCC rešetke, atomi se dotiču
smjerom plošne dijagonale kocke. FCC
rešetka gama-željeza ima brid a = 356,96
pm. Za radijus atoma željeza u gama-željezu
dobivamo:
R(g-Fe) = ¼
× a × √2 =
¼ × 356,96 pm × √2 = 126,20
pm.
Kao što
smo pokazali na primjeru cezijeva
klorida, ponovo možemo zaključiti da atomi nisu krute kuglice stalnih
radijusa.
Radijusi atoma koje nalazimo u tablicama obično su srednje vrijednosti
dobivene
iz većeg broja sličnih kristalnih struktura. Za uspoređivanje i
iskazivanje
radijusa atoma dovoljne su cjelobrojne vrijednosti iskazane u
pikometrima, a
znamenke iza decimalnog zareza su nepouzdane.
4.4.4.
Heksagonska gusta slagalina
Heksagonska
gusta slagalina (HCP - Hexagonal Close Packing) kuglica jednake
veličine
slična je kubnoj najgušćoj slagalini. Na slici 4.17. pokazano je da se
u
najgušćem sloju kuglica jednake veličine oko svake kuglice nalazi šest trokutnih praznina koje smo označili
crvenom i zelenom bojom. U
kubnoj
najgušćoj slagalini slojevi se slažu jedan iznad drugoga tako da
kuglice trećega
sloja dolaze iznad onih trokutnih
praznina u prvome sloju koje nisu bile zauzete kuglicama drugoga sloja.
Prema tome,
u FCC rešetki slojevi kuglica (atoma) slažu se redoslijedom ABCABC....
U heksagonskoj
gustoj slagalini slojevi se ponavljaju redoslijedom ABAB...
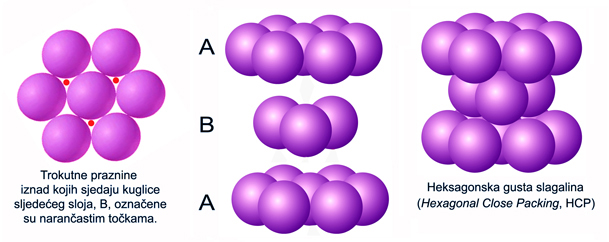
Slika 4.21.
U heksagonskoj gustoj
slagalini slojevi se slažu jedan povrh drugoga tako da kuglice B sloja
sjedaju
iznad trokutnih praznina A sloja. Treći sloj jednak je prvom sloju pa
se slojevi
u heksagonskoj gustoj slagalini ponavljaju redoslijedom ABAB...
Po tipu
heksagonske guste
slagaline kristaliziraju Be, Mg, Sc, Ti, Co, Zn, Cd, Ti, neki drugi
prijelazni
metali i većina lantanoida. Gustoća slaganja jednaka je kao i u FCC
rešetki jer
sa stajališta gustog slaganja, svejedno je slažu li se slojevi
redoslijedom
ABAB ili ABCABC. Tetraedarske i oktaedarske praznine jednake su kao i u
FCC
rešetki, ali su drukčije raspoređene.
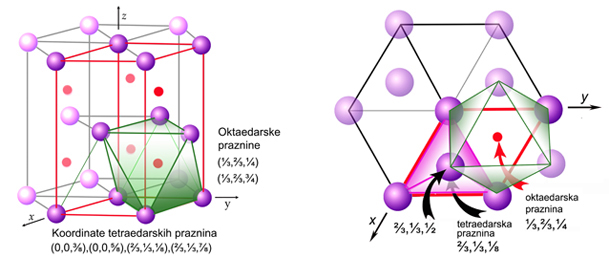
Slika
4.22. Jedinična
ćelija HCP rešetke sadržava dva čvora (atoma); jedan na uglovima
jedinične ćelije
i jedan na koordinati ⅔,⅓,½. Crvene točke označuju položaje
oktaedarskih praznina. U HCP rešetki KB = 12.
Na osnovi
slike 4.22. lako je zaključiti da je visina, odnosno c
os heksagonske prizme, jednaka dvije
visine idealnog tetraedra. Ako je brid tetraedra a
= 1, tad je njegova visina v
= a × √(2
Ukratko,
metali nisu jednostavne slagaline
kuglica. Unutar kristala među atomima metala djeluju usmjerene sile, a
u nekim
se slitinama javljaju vrlo jake kovalentne veze. Primjerice, slitina
koja
sadržava do 35 % cinka u bakru može se kovati, valjati i izvlačiti u
žice. To je
kruta otopina u kojoj je u kristalima bakra (FCC rešetka) dio atoma
bakra statistički
zamijenjen atomima cinka. No, ako se udio cinka poveća na oko 60 %
dobije se slitina
krta poput stakla. Njezin sastav odgovara formuli Cu5Zn8.
To nije smjesa atoma bakra i cinka već pravi međumetalni (intermetalni)
spoj
zasebne kubne kristalne strukture s jasno izraženim kovalentnim vezama.
4.4.5. Defekti u
kristalima
Ne
postoji savršen kristal u kojem bi svi
atomi bili na mjestima zadanim simetrijom kristalne rešetke. Svi realni
kristali
imaju neke nedostatke koji utječu na njihova fizička i kemijska
svojstva. No,
ti nedostaci nisu uvijek nešto loše, naprotiv, namjerno ih izazivamo da
bismo
postigli željena fizička svojstva. Realni
kristali najčešće su mozaične
građe, što znači da se kristal sastoji od idealno građenih blokova, ali
međusobno malo zakrenutih. Moguće su i pogreške u redoslijedu slaganja
slojeva.
Tipičan primjer jest kobalt koji kristalizira po tipu HCP rešetke, ali
se
kojiput "zabuni" u redoslijedu slaganja slojeva, primjerice;
ABABABCABCBABAB...
U kristalima razlikujemo točkaste,
linijske,
površinske i volumne defekte.

Slika
4.23. Shematski
prikaz točkastih defekata u kristalu.
Točkasti defekti su mjesta na kojima atom
nedostaje ili mjesta na koja su se ubacili atomi primjesa. Atom
primjesa može
zamijeniti (supstituirati) regularni atom u kristalu pa govorimo o
supstitucijskim primjesama. Ako se atom primjesa smjesti između
regularnih
atoma, tad govorimo o intersticijskim primjesama. Primjese u
metalima, supstitucijske ili intersticijske, umanjuju električnu
provodnost
metala. Čisti metal uvijek ima najveću provodnost, pogotovo pri nižim
temperaturama. Danas postoji mnogo eksperimentalnih dokaza koji ukazuju
na to
da značajan broj mjesta u kristalu nije zaposjednut atomima. Nadalje,
termodinamičke studije pokazuju da su strukture s praznim mjestima u
kristalu
energijski stabilnija stanja metala.
Frenkelov
defekt u ionskom
kristalu sastoji se od praznoga mjesta i iona koji se
pomaknuo s toga mjesta u neki intersticijski položaj. Taj tip defekata
najviše
je zastupljen u srebrovim halogenidima, AgBr i AgI. Schottkyjev
defekt sastoji se od parova iona koji manjkaju u kristalu
tako da je kristal električki neutralan. Točkasti defekti značajno
utječu na
električnu provodnost krutina.
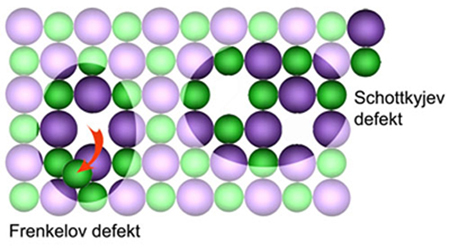
Slika
4.24.
Shematski prikaz Frenkelova i
Schottkyjeva
defekta u ionskom kristalu.
Linijski
defekt ili
dislokacija obuhvaća
velik broj atoma duž linije u kristalu. Promatranjem
pomoću elektronskoga
mikroskopa mogu se uočiti odjednom prekinuti čitavi nizovi ili slojevi
atoma.
Takva mjesta unose naprezanja u kristal. Što je broj takvih dislokacija
veći, naprezanja
u kristalu su veća. Dislokacije
utječu na
mehanička, električna, magnetska, termička i druga svojstva krutina. Površinski defekti su primjerice
granice zrna. Volumni defekt
su primjerice mjehurići zraka/plina zaostali prilikom skrućivanja
taljevine.

Slika
4.25.
Nanokristal paladija promatran pomoću elektronskoga mikroskopa. Uočite
granice
između različito orijentiranih kristalnih zrna. Bijele točke prikazuju
stupce atoma
paladija okomite na sliku. Obratite pozornost na nesređen raspored
atoma na
granicama zrna kao primjer površinskog defekta.
Izvor: https://www.quora.com/Can-atoms-be-seen-under-an-electron-microscope
Zašto
tijekom kristalizacije nastaju defekti u kristalu lako je
razumjeti. Uzmimo primjerice da kristal cezijeva klorida vrlo polagano
raste,
samo 1 mm dnevno. Brid jedinične ćelije cezijeva klorida je: a = 412 pm. Broj slojeva CsCl koji se
tijekom dana izluče na površini kristala dobit ćemo tako da prirast
debljine
kristala, 1 mm, podijelimo duljinom brida jedinične ćelije CsCl, pa
dobivamo:
N(CsCl) = 10‒3
m/412×10‒12 m = 2,4×106.
Kako dan ima 86 400 s, proizlazi da se svake sekunde na površinu
kristala nadogradi
28 slojeva jediničnih ćelija cezijeva klorida. Uzmemo li još u obzir i
primjese
prisutne u otopini, uz takvu brzinu nadogradnje kristala nemoguće je
izbjeći
dislokacije.
Mehanička
svojstva pojedinog
metala ne ovise samo o prirodi kemijske veze među njegovim
atomima, već i o prethodnoj termičkoj i mehaničkoj obradi. Primjerice,
bakar
ugrijan do crvenog usijanja nakon hlađenja je mekan i može se
oblikovati kovanjem.
No, tijekom kovanja bakru se drastično poveća tvrdoća jer se kristalna
zrna
smanje, a u njih se unesu brojne dislokacije. U povećanje tvrdoće
metala nakon
hladne obrade kovanjem možete se uvjeriti jednostavnim pokusom. Uzmite
komad
deblje bakrene žice, promjera 4 ili 5 mm, ili tanju bakrenu cijev
promjera 6 mm
i duljine oko 30 cm. Uzorak žice ili cijevi užarite u plamenu plinskoga
plamenika. Kad se cijev ohladi savijte je rukama, a onda je pokušajte
na istom
mjestu izravnati. Savijanjem ste unijeli dislokacije u kristale bakra
što
otežava klizanje slojeva. Ponovo užarite cijev i ohladite pod vodom.
Nakon
žarenja cijev će opet postati mekana. Pri temperaturi crvenog usijanja
atomi
osciliraju velikom amplitudom oko ravnotežnih položaja. To im omogućuje
da se
slože na najgušći mogući način u što veće kristale jer je to energijski
povoljnije. Time se smanjuje broj dislokacija pa bakar ponovo postaje
mekan i
prikladan za daljnju hladnu obradu kovanjem. Na slici 4.26.a prikazan
je izgled
zrna slitine bakra s 30 % cinka prije i nakon mehaničke obrade
valjanjem. Slitina
bakra s 30 % cinka je kruta
otopina cinka u
bakru i kristalizira po tipu FCC rešetke. Tamnija i svjetlija mjesta
(pruge) unutar
većih zrna ukazuju na različitu orijentaciju kristalića unutar zrna.
Različite kristalne
plohe u FCC rešetki različito su zaposjednute atomima cinka i bakra i
zato se različitom
brzinom otapaju dušičnom kiselinom. Jače nagrizene plohe slabije
reflektiraju
svjetlost pa ih zato vidimo kao tamnija ili različito obojena područja.
Slika
4.26.b pokazuje da se tijekom valjanja kristalna zrna izduže, a tamnije
linije
unutar zrna ukazuju na smjer klizanja slojeva unutar kristala.

Slika
4.26. a)
Izgled površine slitine bakra s 30 % cinka nakon poliranja i nagrizanja
dušičnom
kiselinom. Uzorak je prethodno bio ugrijan do crvenoga usijanja i
polagano
ohlađen na sobnu temperaturu. b) Isti uzorak nakon hladnog valjanja pri
čemu se
njegova tvrdoća poveća
zbog nastajanja
dislokacija. Izvor: https://vacaero.com/information-resources/metallography-with-george-vander-voort/1440-deformation-and-annealing-of-cartridge-brass.html
Pri
kovanju metala ne dolazi odjednom do klizanja čitavih slojeva,
nego se pomiču dislokacije unutar slojeva. To je energijski povoljnije.
Slika 4.27.
prikazuje kako jedna dislokacija, koju čini skupina atoma, putuje od
jednog
kraja kristala na drugi što rezultira pomakom čitavog sloja.
Slika 4.27. Shematski prikaz pomaka slojeva u kristalu metala pod utjecajem mehaničke sile. a) Uočite položaj atoma označenih točkom u početnom stanju. b) Dislokacija koja se stvori na jednom kraju kristala premješta se od atoma do atoma (slika c) dok ne izađe na drugom kraju kristala (slika d). Konačan je rezultat međusobni pomak slojeva, kao što pokazuje položaj atoma označenih točkom.
Pomak
dislokacija u kristalu možemo usporediti s pomakom nabora na
dugačkom prostiraču. Ako se na prostiraču pojavi nabor, za izravnavanje
nabora
moramo odjednom povući čitav prostirač. Za takav zahvat treba odjednom
uložiti
velik rad. Moguće je i drugo energijski povoljnije rješenje. Nabor
treba gurati
od jednog prema drugom kraju prostirača. To se može učiniti s više
manjih
obroka energije.
4.4.6. Fazne pretvorbe
Tvari se
javljaju u različitim agregacijskim
stanjima: plinovitom, tekućem ili krutom. Agregacijsko stanje tvari
ovisi o
tlaku i temperaturi. No, neki kemijski elementi i spojevi mogu u krutom
stanju imati
različitu kristalnu strukturu (rešetku), što ovisi o temperaturi i
tlaku. Već
smo to pokazali na primjeru željeza. Iznad 912 oC
željezo
kristalizira po tipu FCC rešetke, a ispod te temperature po tipu BCC
rešetke. Pritom
dolazi i do promjene koordinacijskog broja atoma. U FCC rešetki KB =12,
a u BCC
rešetki KB = 8. Temperaturu 912 oC nazivamo
temperaturom fazne
pretvorbe, faznog prijelaza, ili fazne transformacije. Pri svakoj faznoj
pretvorbi dolazi do pomaka atoma
ili molekula.
No, svako micanje ili pregrupiranje atoma ne mora biti fazna pretvorba.
Pokazali
smo to na primjeru savijanja bakrene žice ili štapa. Tijekom
zagrijavanja bakra
dolazilo je do rasta kristalnih zrna i pomaka atoma u kristalu. Pri
savijanju
štapa od bakra opet dolazi do pomaka atoma, unošenja dislokacija u
kristalna
zrna i usitnjavanja zrna. To sve nisu fazne pretvorbe jer se FCC
kristalna
rešetka bakra tijekom mehaničke deformacije ne mijenja.
Fazna
pretvorba odnosi se
na promjenu kristalne strukture. Zanimljiv primjer fazne
pretvorbe nalazimo u slitini nikla i titanija u kojem su Ni i Ti u
približnom
omjeru 1 : 1. Ta se slitina naziva "nitinol"
i
jedna je od petnaestak sličnih slitina koje pamte početni oblik (SMA - Shape Memory
Alloys). Nitinol je
intermetalni
spoj koji pri visokoj temperaturi ima kubnu kristalnu rešetku tipa
cezijeva
klorida. To znači da se atomi titanija nalaze u središtu kocke koju
čine atomi
nikla, i obratno. Ako se od takve slitine načini opruga i ugrije na oko
500 oC,
opruga će trajno zadržati oblik. No, hlađenjem na sobnu temperaturu
dolazi do
fazne pretvorbe, tj. kristalna struktura se promijeni iz kubne u
monoklinsku. U
kubnoj kristalnoj rešetki sve tri osi su jednake, a kutovi među osima
iznose 90o.
U monoklinskoj kristalnoj rešetki sve tri osi su različite duljine, a
jedan se
kut među osima razlikuje od 90o. Opruga je
zadržala svoj oblik bez
obzira na promjenu kristalne strukture. Tako ohlađena opruga može se
rastezanjem deformirati. Kad se deformirana opruga uroni u vruću vodu
ona opet poprimi
svoj prvotni nedeformirani oblik. Malim promjenama sastava slitine
temperatura prijelaza
nitinola u izvorni oblik može se kontrolirati u rasponu od oko -20 oC
do 110 oC. Pogledajte na Internetu: https://www.youtube.com/watch?v=s62PL5vmfNw
https://www.youtube.com/watch?v=wI-qAxKJoSU
https://www.youtube.com/watch?v=-K57cbOhA5g
https://education.mrsec.wisc.edu/memory-metal/
Slitine
koje pamte početni oblik, SMA ili memorijski metali, imaju
mnogobrojne primjene. U kirurgiji se rabe kod prijeloma kostiju, u
ortodonciji
za ispravljanje zuba, kod kardiovaskularnih bolesti rabe se za stentove za
proširenje suženih krvnih žila, kao i za druge medicinske svrhe.
Suvremene miješalice
tople i hladne vode za tuširanje imaju ugrađene opruge od memorijskih
metala
koje održavaju stalnu temperaturu vode. Rabe ih u sustavima za zaštitu
od požara
tako da se pri porastu temperature automatski zatvaraju ventili za
dovod plina
ili zapaljivih tekućina. Rabe se u avijaciji, astronautici, robotici i
drugim
naprednim tehnologijama.
Doznajte više na: https://saylordotorg.github.io/text_general-chemistry-principles-patterns-and-applications-v1.0/s16-solids.html
http://www.azoo.hr/images/stories/dokumenti/Gradja_tvari.pdf
Željezo i njegove slitine s elementima prijelaznih skupina periodnog sustava elemenata temeljni su materijal za suvremene metalne konstrukcije, predmete svakodnevne uporabe, strojogradnju, brodogradnju, željeznice itd. Iako nam se čini da o željezu sve znamo, ipak, industrijski razvijene zemlje imaju brojne institute koji se bave samo željezom. No, aluminij, magnezij, titanij, skandij, kao i njihove slitine zanimljivi su za avijaciju, astronautiku, i one primjene gdje se traži što manja masa konstrukcije. Svaki metal ili njegova slitina danas ima neku tehničku primjenu. Zato se istraživanjem metala i njihovih slitina bave mnogi znanstveni instituti i sveučilišta. Pri istraživanju kristalnih struktura metala i slitina uz ostale fizičke metode važnu ulogu ima difrakcija rendgenskih zraka u kristalu čime ćemo se pozabaviti u sljedećem poglavlju.
5. X-zrake
Wilhelm
Conrad Röntgen
(1845. – 1923.), profesor fizike na Sveučilištu u Würzburgu, tijekom
1895.
godine poput brojnih fizičara
(William Crookes,
Heinrich Hertz, Johann Hittorf, Julius
Plücker, Eugen
Goldstein, Philipp
von Lenard, Kristian
Birkeland, Mihajlo
Pupin, Nikola Tesla, Ivan Puluj i
drugi) ispitivao
je utjecaj visokog napona na
električno pražnjenje u razrijeđenim plinovima i u vakuumskim cijevima.
U
studenom 1895. Röntgen
je
bio zaokupljen istraživanjem katodnih zraka. Pritom je
koristio uređaje dostupne u bilo kojem sveučilišnom
laboratoriju: induktor s elektromagnetskim prekidačem, vakuumske
cijevi i fluorescentni zaslon. Izvodio je eksperimente s jednom od Lenardovih
cijevi s
tankim aluminijskim prozorom koji je omogućio da katodne zrake izlaze
iz
cijevi. Kasno poslijepodne 8. studenoga 1895. omotao je vakuumsku cijev
crnim
papirom. Nakon uključivanja induktora u zamračenoj sobi primijetio je
svjetlucanje
malih kristala barijeva tetracijanoplatinata(II) tetrahidrata,
(Ba[Pt(CN)4]∙4H2O), koji su bili u
blizini. Röntgen je sumnjao na novu
vrstu zračenja. Nije rekao nikome o svom otkriću. Umjesto toga, proveo
je
sljedećih sedam tjedana u laboratoriju istražujući nove zrake i njihova
svojstva.
28.
prosinca 1895. Röntgen je Fizičkom zavodu Sveučilišta u Würtzburgu
podnio izvješće o novoj vrsti zraka (Ueber
eine neue Art von Strahlen) kojem je bio priložen snimak ruke
gospođe
Röntgen na fotografskoj ploči. X-zrake, kako ih je Röntgen nazvao,
izazivaju
fluorescenciju, prolaze kroz tvar, izbijaju elektroskop, ali se ne
otklanjaju u
magnetskom polju. To je izvješće tiskano 05. 01. 1896. U ožujku 1986.
objavio
je drugu i godinu dana kasnije u ožujku 1887. treću i konačnu
publikaciju o
X-zrakama. U trećoj publikaciji iz ožujka 1887. Röntgen govori o
opetovanim
pokušajima difrakcije X-zraka, ali kako sam navodi nije uspio
registrirati niti
jedan eksperiment iz kojeg bi sa zadovoljavajućom sigurnošću mogao
dobiti
dokaze o postojanju ogiba
(difrakcije)
X-zraka. Fizička svojstva X-zraka u doba njihova otkrića bila su
nepoznata.
Jedni su znanstvenici smatrali da su čestične ili korpuskularne (lat. corpusculum
- tjelešce, sitna čestica), a drugi valne prirode. Naime,
mehaničkim
putem nije bilo moguće načiniti optičku
rešetku na kojoj bi
se pokazao ogib X-zraka i tako dokazala njihova valna svojstva.
Naziv X-zrake zadržao se u anglosaksonskim zemljama, a naziv rendgenske
zrake
uobičajen je u Europi.
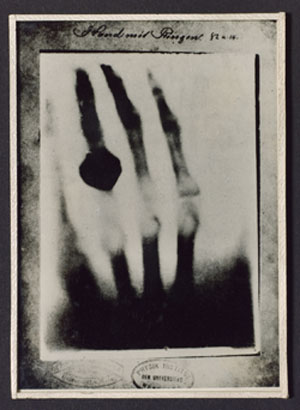
Slika 5.1. Slika ruke gospođe Röntgen snimljena 22. 12. 1895. Kad je vidjela sliku, rekla je: "Vidjela sam svoju smrt." Izvor: https://en.wikipedia.org/wiki/X-ray
U roku od
mjesec dana nakon objavljivanja otkrića X-zraka u Europi i
Sjedinjenim Američkim Državama načinjeno je nekoliko medicinskih
radiografija (rendgenografija,
rendgenskih slika) koje su kirurzi koristili u svom radu, a već nakon
6 mjeseci liječnici na bojišnicama rabili su X-zrake
za pronalaženje metaka u ranjenim vojnicima.
Doznajte
više na:
https://en.wikipedia.org/wiki/Crookes_tube
https://www.lernhelfer.de/schuelerlexikon/physik-abitur/artikel/wilhelm-conrad-roentgen
https://www.iucr.org/publ/50yearsofxraydiffraction/full-text/x-rays
5.1.
Otkriće i svojstva X-zraka
O otkriću
X-zraka napisano je mnogo tekstova. Danas neki tvrde da su
X-zrake prije Röntgena otkrili i drugi znanstvenici, primjerice Nikola Tesla
(1876. -
1943.) i Ivan Puluj
(1845. -
1918.) znanstvenik ukrajinskog podrijetla poznat po pionirskom radu na
istraživanju
katodnih zraka.
Ivan
Puluj diplomirao je na Teološkom fakultetu Sveučilišta u Beču. Kasnije
se
upisao na odjel za fiziku i matematiku Filozofskog fakulteta na istom
Sveučilištu
na kojem je od 1869. do 1874. bio asistent. Od 1874. do 1875. godine predaje fiziku na Vojnoj
pomorskoj
akademiji u Rijeci.
Kao stipendist austrijskog
Ministarstva obrazovanja 1875.
godine odlazi na stručno usavršavanje kod prof. Augusta Kundta na Sveučilištu u Strasbourgu. Tamo je upoznao
Röntgena, asistenta prof. Kundta. Puluj se zainteresirao za fenomen električnog
pražnjenja u razrijeđenim plinovima i vakuumskim cijevima.
Nakon
što je naučio staklopuhačko umijeće izrađivao je
staklene cijevi za vlastite pokuse i za potrebe drugih fizičara. Nikola
Tesla, koji
je također trenutačno boravio u laboratoriju profesora A. Kundta,
sprijateljio
se s Ivanom Pulujem te su zajedno načinili niz pokusa s električnim
pražnjenjem
u razrijeđenim plinovima i vakuumskim cijevima. Puluj je u
Strasbourgu doktorirao 1876. Nakon povratka na Sveučilište u Beču
nastavio je istraživati
katodne zrake i između 1880. i 1882. godine objavio nekoliko radova. Na
temelju
tih istraživanja konstruirao je svjetiljku
s antikatodom
položenom pod kutom od 45o u odnosu na snop
katodnih zraka. Antikatodu
je premazao fluorescentnim materijalom, primjerice smjesom kalcijeva i
bakrova
volframata, CaWO4 + CuWO4.
Svjetiljka, za koju je dobio
srebrnu medalju na Međunarodnoj elektrotehničkoj izložbi u Parizu
1881., davala je
"hladno svjetlo". Jednu
takvu svjetiljku Puluj je poklonio i
Röntgenu. Puluj je primijetio da fotografske ploče
pocrne ako se nalaze u blizini njegove
svjetiljke ili cijevi s katodnim zrakama. U stvarnosti, ta je
svjetiljka bila
izvor tada nepoznatih X-zraka koje Puluj nije prepoznao premda je
svojim
studentima demonstrirao slike ruke
i
prstiju, dobivene pomoću njegove cijevi/svjetiljke. Rezultate pokusa sa
svjetiljkom Puluj je objavio u Zeitschrift Wien
Akademie
(1880-1882). Ivan Puluj prvi je u svijetu (1895. god.)
fotografirao i dobio vrlo jasne "rendgenske"
slike slomljene ruke 13-godišnjaka i ruke svoje kćeri s metalnom iglom
ispod
nje.
Doznajte
više na:
https://www.crtsite.com/R-2_Savchuk-3.pdf
http://mirtiens.ru/vtu59xeozybai66/Пулюй,_Иван_Павлович
http://wiki.ciit.zp.ua/index.php/%D0%9A%D1%82%D0%BE_%D0%92%D1%8B,_%D0%98%D0%B2%D0%B0%D0%BD_%D0%9F%D0%B0%D0%B2%D0%BB%D0%BE%D0%B2%D0%B8%D1%87_%D0%9F%D1%83%D0%BB%D1%8E%D0%B9%3F
https://prezi.com/gsnomhpzmde5/ivan-puluj/
http://www.crtsite.com/page5.html
https://wikivisually.com/wiki/Ivan_Puluj
Ubrzo
nakon što je saznao za Röntgenovo otkriće X-zraka Puluj je pisao
Röntgenu i pitao ga je li u svom istraživanju upotrijebio njegovu
svjetiljku?
No, pitanje je ostalo bez odgovora. Nekoliko dana nakon toga, 13.
veljače 1896.
Puluj je objavio
rad: Podrijetlo rendgenskog zračenja, njegovo
fotografsko djelovanje, u kojem je pokazao da X-zrake nastaju
kao rezultat međudjelovanja
negativno nabijenih čestica (katodnih zraka) s atomima antikatode. To
je važno
za razumijevanje mehanizma nastajanja X-zraka, o čemu Röntgen i drugi
istraživači ne govore niti jednu riječ. U siječnju 1896. Puluj je već
napravio
niz visokokvalitetnih fotografija i pokazao mogućnost korištenja
X-zraka u
medicinskoj dijagnostici u što Röntgen nije vjerovao jer je za
dobivanje slike
objekt morao eksponirati 40 do 50 minuta. No, Puluj je sa svojom cijevi
s
antikatodom položenom pod kutom od 45o to
vrijeme skratio na 2 do 5
sekundi. Takav dizajn antikatode omogućio je dobivanje
snopa
X-zraka velikog intenziteta i visoku kvalitetu slika.
Još
1892.g. u jednom predavanju Tesla je izvijestio da primjenom
snažnog visokofrekventnog i visokonaponskog napajanja iz različito
oblikovanih Crooksovih cijevi vlastite
izrade izlaze vidljiva svjetlost, "crna svjetlost" (ultraljubičaste
zrake) i "posebne zrake" (engl. very
special radiation) koje uzrokuje sjene na fotografskim
pločama pohranjenima
u metalnim kutijama u njegovom laboratoriju. Nažalost, Tesla je morao
prekinuti
svoja istraživanja "posebnih zraka" zbog požara u laboratoriju 15.
ožujka 1895. Pritom je uništena sva oprema i laboratorijske bilješke.
Svojstva Teslinih
"posebnih zraka" bila su jednaka svojstvima X-zraka W.C. Röntgena.
Neposredno
po objavljivanju otkrića X-zraka Tesla je pisao Röntgenu o svojem
višegodišnjem
istraživanju "posebnih zraka". Vidjevši sjene na fotografskoj ploči
Teslinih zraka koje su prošle kroz neke predmete,
Röntgen je Tesli odgovorio da su njegovi
pokusi izuzetno zanimljivi, te ga zamolio da mu opiše način kako je
dobio svoje
"posebne zrake".
Tesla je
detaljno opisao svoje eksperimente u nizu radova objavljenih
u časopisu Electrical Review, New York,
a prvi od tih radova objavljen je već 11. ožujka 1896. U radovima iz
1896.
godine predvidio je da X-zrake imaju svojstva svjetlosti tj. da su to
elektromagnetski valovi. Tesla je prvi
upozorio na štetnost
X-zraka. Protekom vremena pojavljivalo se sve više izvješća o
oštećenjima
očiju, kože, ispadanju kose i oboljenjima liječnika koji su u
dijagnostici rabili
rendgenske uređaje bez odgovarajuće zaštite.
Osim
Tesle i Puluja Röntgenove pokuse odmah su mogli ponoviti mnogi
znanstvenici u Europi, Americi i carskoj Rusiji. No, Röntgen je prvi
objavio
svoje otkriće i njemu pripada prioritet te je 1901. godine za to
otkriće dobio
prvu Nobelovu nagradu za fiziku. Tesla i Puluj nikad nisu Röntgenu
osporavali
prioritet otkrića X-zraka.
Doznajte
više:
S.
POPOVIĆ, Nikola Tesla, znanstvenik i izumitelj – otkriće X-zraka, Matematičko fizički list 64,
br. 4(2013/2014) 241 - 250.
https://pubs.rsna.org/doi/10.1148/rg.284075206
http://anengineersaspect.blogspot.hr/2014/02/the-ray-of-mystery-x-ray-news-from-1896.html
https://www.rtl.hr/kbc/novosti/2652345/sto-je-rendgen/
U
produžetku pročitajte zanimljiv odlomak što ga je o otkriću
rendgenskih zraka napisao akademik Ivan Supek (1915. - 2007.) u knjizi:
Od antičke filozofije do moderne nauke o
atomima, Nakladni zavod Hrvatske, Zagreb 1946. str. 210 -
212.
Novembra 1895. sjedio je kasno u
noći profesor fizike Röntgen uz
katodnu cijev i studirao elektronske zrake. Katodnu cijev koja je
svijetlila
prekrio je crnim papirom da svjetlost ne dopre napolje. U sobi je bila
potpuna
tama. Najedanput opazi da na stoliću pokraj njega svjetlucaju
kristalići
izvjesnog kemijskog spoja. On se začudi. Što pobuđuje kristaliće na
svjetlucanje? Staklo katodne cijevi bilo je debelo i elektroni su
izlazili
napolje samo kroz poseban prozorčić. Röntgen uhvati knjigu pored sebe i
stavi
je ispred kristalića. Oni su i dalje svjetlucali. Knjigu zamijeni
drvom, krpom,
metalom. Svejedno.
Od
te noći Röntgen
nije stigao pravo ni da jede ni spava. Živio je u uzbuđenju i groznici.
Zatvorio se u svoj laboratorij. Pred svima, pa i svojim asistentima,
tajio je što
je opazio. Nekoliko tjedana iza toga izdaje svoju fundamentalnu
raspravu
"Jedna nova vrst zraka".
Nove zrake mogu se ustanoviti po tome
što pobuđuju na svjetlucanje razne supstancije ili zacrne fotografsku
ploču.
Röntgen je opazio da one izlaze iz mjesta u cijevi na koje padaju
katodne
zrake. Njihov postanak mora dakle biti u uskoj vezi s kočenjem katodnih
zraka u
staklu. One se razlikuju od katodnih zraka. Ni jakim magnetom nije ih
Röntgen
mogao svinuti. Pored toga mnogo su prodornije od svih poznatih zraka.
Röntgen
je stavljao debele ploče od drva i tanke listiće metala pred zrake, i
one su
prošle skroz. Ako je debljina prevelika, zrake prestaju. Pri tome
opazio je da
ih jače apsorbiraju elementi s većom atomskom težinom. Teško olovo
mnogo jače ugušuje
nove zrake od vode.
Röntgen je stavio ruku između katodne
cijevi i fotografske ploče. Zagonetne su zrake prošle kroz ruku i pale
na
ploču. Na slici su se vidjele kosti ruke. Kosti su poglavito građene od
kalcija
pa jače apsorbiraju zrake nego meso. One bacaju "sjenu". Na taj način
mogle su se fotografirati kosti u unutrašnjosti našeg tijela.
Otkriće je bilo senzacionalno. Otvorena
je bila nova epoha u medicini. Röntgenske zrake postale su prodornim
okom
kirurgije. Liječnik je sad prije operacije mogao vidjeti što treba da
reže.
Doskora su röntgenske zrake našle primjenu i u drugim medicinskim
granama.
Röntgenske slike kostura ostavile su
dubok dojam u javnosti. Mnogi nijesu mogli spavati kad su vidjeli
mrtvačku
viziju svoje glave na slici. Röntgensko oko gledalo je kroz kožu i
meso. Bilo
je nešto jezivo u tome. Kako građani obično ne razumiju o čemu se u
nauci radi,
mnogi su pomislili da će se sada moći prozreti ljudska unutrašnjost
zajedno s
mislima i osjećajima. Ljudi u svojem stanu nijesu se više osjećali
sigurni od
tuđe radoznalosti. Što koristi debeo zid kad zrake svuda prolaze? Mudri
američki poslanik Reed tražio je 1896. poseban zakon protiv ovih
nepoželjnih
zraka. Neki vješti trgovac u Londonu iskoristi opću psihozu pa počne
prodavati
rublje koje zaštićuje od röntgenskih zraka. Djevojačka stidljivost bila
je
ugrožena. Godinu dana iza toga, kako to već uvijek biva, buka se
stišala i novo
je otkriće izgubilo čar.

Slika 5.2. Nova rendgenska fotografija: Life, veljača 1896.
Rendgenske
zrake ubrzo su našle primjenu u
medicini što je potaknulo razvoj rendgenske opreme, snažnih rendgenskih
cijevi
i generatora visokog napona. Unatoč velikom interesu za rendgenske
zrake i
velikom broju fizičara koji su ih istraživali, samo je nekoliko
temeljnih
činjenica otkriveno u sljedećih petnaest godina, od kojih ćemo
spomenuti samo dvije:
1. Charles Glover Barkla
(1877. –
1944.) britanski fizičar (dobitnik Nobelove nagrade za fiziku 1917.
godine) tijekom
1905. godine otkrio je polarizaciju rendgenskih zraka i pokazao da su
one
elektromagnetski valovi slični običnoj svjetlosti.
2.
Tijekom 1909. godine Barkla je uočio karakteristično rendgensko
zračenje. Naime, u to doba rendgenske zrake razlikovali su prema
njihovoj
"tvrdoći". Povišenjem napona na rendgenskoj cijevi dobivale su se
prodornije rendgenske zrake. Pritom je ustanovio dvije vrste zračenja.
Mekano ili
bijelo zračenje apsorbira se u prvim slojevima apsorbera i nema
konstantan
apsorpcijski koeficijent. Eksperimentirajući s različitim naponima i
rendgenskim
cijevima s različitim anodama, ustanovio je da rendgenske zrake
sadržavaju
jednu snažnu "karakterističnu" homogenu komponentu s konstantnim
apsorpcijskim koeficijentom. Nadalje, ustanovio je da se apsorpcijski
koeficijent "karakterističnog" rendgenskog zračenja smanjuje s
porastom rednog broja elementa anode rendgenske cijevi.

Slika 5.3.
Rendgenske
zrake nastaju kočenjem ubrzanih elektrona u materijalu anode. Na slici
je
prikazana ovisnost spektra rendgenskih zraka o naponu na cijevi s
molibdenskom
anodom. Pri nižem naponu dobije se kontinuirano ili zakočno rendgensko
zračenje, a tek pri višem naponu pojavljuje se karakteristično
zračenje. U doba
kad je Barkla otkrio karakteristično zračenje, valna duljina
rendgenskih zraka nije
bila poznata. Prije toga, 1907. godine, Willy Wien (1864. – 1928.) je
na
temelju još nepotpunih spoznaja o fotoefektu, za pretpostavljeni napon
od 20 000
V, izračunao valnu duljinu rendgenskog zračenja λ = 0.05 nm.
(Slika izvor: http://www.physics.brocku.ca/PPLATO/h-flap/phys8_3.html)
5.2.
Difrakcija rendgenskih zraka
Na
poziv
bavarske vlade Röntgen je 1900. godine prešao u München u svojstvu
ravnatelja Instituta
za
eksperimentalnu fiziku Sveučilišta u Münchenu. Godine
1912., osim
Röntgena, na tom su Sveučilištu djelovali znameniti njemački mineralog Paul
Heinrich Ritter von Groth
(1843. –
1927.) i Arnold Sommerfeld
(1868. – 1951.),
njemački fizičar i matematičar. Svaki
od njih bio je
ravnatelj instituta s asistentima, predavačima (Privatdozenten)
ili izvanrednim profesorima te drugim pridruženim osobljem.
Röntgenov institut bio je najveći s brojnim studentima, asistentima i
predavačima. Röntgen je imao 12 do 15 doktoranada, a među njima bio je i
Walther Friedrich. (1883. – 1968.).
Sommerfeldov
institut za teorijsku fiziku bio je najmanji i osnovan
tek 1906. godine. Krajem 1911. na Sommerfeldovom institutu za asistenta
imenovan je Walther
Friedrich (1883. -
1968.) koji je upravo završio doktorsku disertaciju u
susjednom Institutu za eksperimentalnu fiziku pod vodstvom Röntgena.
Imao je
dragocjeno znanje o rendgenskim zrakama i iskustvo u radu s rendgenskom
opremom. Na Sommerfeldovom institutu bio je i Peter
Paul Ewald
(1888. – 1985.) koji je 1912. godine
radio na matematičkoj interpretaciji prolaza svjetlosti kroz kristale
za koje
se pretpostavljalo da sadržavaju strogo uređeni prostorni razmještaj
čestica. Max
von Laue
je od 1909. do 1912. bio
privatni docent na
istom Institutu za teorijsku fiziku gdje predaje optiku, termodinamiku
i
teoriju relativnosti. Zahvaljujući nastojanjima kristalografa Paula von
Grotha mnogi
instituti na Sveučilištu u Münchenu imali su modele "sumnjivih" Bravaisovih
prostornih rešetki, za koje još nitko
nije dokazao da kristali imaju baš takvu strukturu.
U jednom
neformalnom razgovoru Laue je zapitao Ewalda što će se
dogoditi ako valna duljina svjetlosti bude manja od razmaka među
atomima, a ne
mnogo veća, kao što je slučaj s vidljivim svjetlom. Kad je Ewald
strukturu kristala
opisao kao periodički razmještaj rezonatora koji imaju udaljenost
usporedivu s
pretpostavljenom valnom duljinom rendgenskih zraka, Laue je pomislio da
bi
karakteristične fluorescentne X-zrake, nastale od teških čestica (atoma
metala)
u kristalnoj strukturi, mogle proizvesti difrakcijske slike.
Sommerfeld
i Wien
bili su skeptični kad im je Laue
predložio eksperiment. Kako teoretičar Laue može biti tako hrabar da
ponavlja eksperiment
koji je već načinio Röntgen? Nadalje, Sommerfeld je smatrao da ne
postoji
međusobna zavisnost faza fluorescentnog zračenja emitiranog različitim
točkama
(atomima) u kristalu i zato neće doći do interferencije. Naime, Laue
nije vidio
kristal kao difrakcijsku rešetku za primarne X-zrake, već je očekivao
da će
primarno zračenje potaknuti teške atome u kristalu na fluorescenciju
karakterističnih
X-zraka koje će onda proizvesti difrakcijsku sliku. Ipak, Sommerfeld je
dopustio da se načini eksperiment.
Laue je našao dva sjajna
eksperimentatora, Walthera Friedricha
i Röntgenovog
studenta Paula Knippinga (1883. – 1935.) koji su odlučili
provesti eksperiment. Pokus su izveli s kristalom modre galice, CuSO4·5H2O.
U početku su fotografsku ploču postavili između rendgenske cijevi i
kristala očekujući
difrakcijske slike kako je Laue pretpostavio. Kad je rezultat izostao Friedrich i Knipping došli su do zaključka da će možda
bolji rezultat
postići
stavljanjem ploče iza kristala.
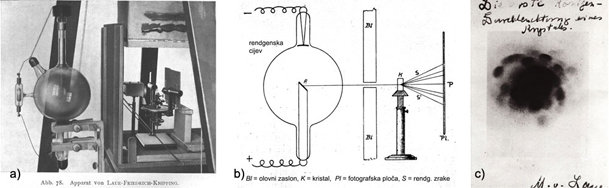
Slika 5.4.
a) Uređaj koji su 1912. g. načinili W. Friedrich i Röntgenov student P.
Knipping.
b) Shematski prikaz eksperimenta. c) Prvu uspješnu difrakcijsku sliku
Friedrich
i Knipping načinili su 23. travnja 1912. Izvor: https://www.iucr.org/__data/assets/pdf_file/0010/721/chap4.pdf
Doznajte
više na:
https://onlinelibrary.wiley.com/doi/pdf/10.1002/andp.201200724
U
narednim pokusima Friedrich i Knipping puštali
su uzak snop rendgenskih zraka kroz tanke pločice dobivene kalanjem
kristala
cinkova sulfida, ZnS, natrijeva klorida, NaCl i galenita, PbS. Kad su
kristale
orijentirali tako da je snop rendgenskih zraka kroz kristal prolazio
smjerom
osi četvrtoga, odnosno trećega reda, na fotografskoj ploči postavljenoj
iza
kristala nakon razvijanja dobili su uređen niz zacrnjenih mrlja.
Dobivene difrakcijske
slike (Lauegrami) pokazivale su istu
simetriju kao i kristali.
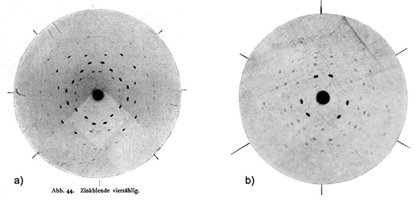
Slika 5.5.
Difrakcijske
slike dobivene prolazom uskog snopa rendgenskih zraka kroz tanke
pločice
cinkova sulfida: a) smjerom osi četvrtoga reda, b) smjerom osi trećega
reda.
Doznajte više na:
https://www.nature.com/articles/090306d0.pdf
5.3.
Kristalna rešetka i mrežne ravnine
Kristalnom
rešetkom opisujemo zakonitost po kojoj se razmještaj
istovrsnih točaka (atoma, iona ili molekula) periodički ponavlja u
prostoru i
to u tri smjera koje smo nazvali kristalografskim osima (vidi slike 4.3. i 4.4.). U
svakoj kristalnoj
rešetki možemo zamisliti niz međusobno paralelnih ravnina jednakoga
međurazmaka. Sve ravnine tog niza sadržavaju iste čvorove kristalne
rešetke
(atome, ione, molekule). Takav niz mrežnih ravnina, sa stalnim
međurazmakom, dhkl,
nazivamo skupom mrežnih
ravnina i označujemo indeksima (hkl).
Niz svih ekvivalentnih skupova mrežnih ravnina, koje sadržavaju
iste čvorove kristalne rešetke i jednake međumrežne razmake, označujemo
{hkl}, na pr. skupovi mrežnih
ravnina paralelnih
svim plohama oktaedra označuju se {111}.
Ako
kristalnu rešetku projiciramo tako da jedna os, primjerice c, bude okomita na ravninu papira, tad
će se sve točke koje leže na osi c
projicirati kao jedna točka. Kroz rešetku projiciranu uzduž osi c može se položiti mnogo skupova mrežnih
ravnina tako da sve ravnine sadržavaju jednake točke (atome). Kako su
te
zamišljene ravnine paralelne s osi projekcije, c,
tad se one projiciraju kao paralelni pravci s konstantnim
razmakom dhk0
. Uočite da
su razmaci između mrežnih ravnina u pojedinim skupovima mrežnih ravnina
različiti i ovise u smjeru u kojem su ravnine položene u odnosu na
kristalografske osi kao što se vidi sa slike 5.6.b.
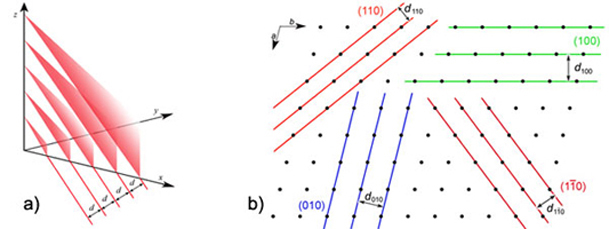
Slika 5.6. a) Skup mrežnih ravnina s konstantnim razmakom dhkl. b) Projekcija kristalne rešetke uzduž osi c. Sve mrežne ravnine paralelne s osi c imaju Millerove indekse (hk0). Razmaci među ravninama s različitim indeksima (hk0) međusobno se razlikuju.
5.4.
Braggov zakon
Za Laueov
eksperiment zainteresirali su se 22. godišnji William
Lawrence Bragg
(1890. – 1971.), koji je studirao fiziku na Trinity
College, Cambridge, i njegov otac William
Henry Bragg (1862. –
1942.), profesor fizike na Sveučilištu u Leedsu. William Henry
Bragg, otac, bio je uvjeren da su rendgenske zrake čestice koje prolaze
kroz
kanale u kristalu. S druge strane mladi Lawrence, prisjećajući se
predavanja
profesora optike, predložio je drukčije tumačenje eksperimenta u
Münchenu. Zbog
ovalnog presjeka snopa "reflektiranih" zraka shvatio je da
“refleksija” rendgenskih zraka nije površinska pojava kao kod
svjetlosti. Na
sjednici Cambridge Philosophical Society
11. studenoga 1912. William Lawrence Bragg objasnio je Laueov
eksperiment kao "refleksiju"
rendgenskih zraka na skupu međusobno paralelnih mrežnih ravnina
zaposjednutih
atomima.

Slika 5.7. "Refleksija"
rendgenskih zraka na skupu mrežnih ravnina zaposjednutim atomima.
Izvor: http://www.amg122.com/twobraggs/firstpaper-mini.pdf
(str.
56)
Polazeći
od Haüy-evih molekula sastavljačica i Bravaisovih rešetki Lawrence
Bragg je shvatio da atomi u kristalima leže u ravninama paralelnim s
plohama
kristala. Međusobno jednako udaljene paralelne ravnine (slika 5.8.a)
zaposjednute atomima mogu poslužiti kao optička rešetka za rendgenske
zrake. Zrake
"reflektirane" od paralelnih ravnina pod određenim kutom bit će u
fazi pa će doći do konstruktivne interferencije (slika 5.8.b).
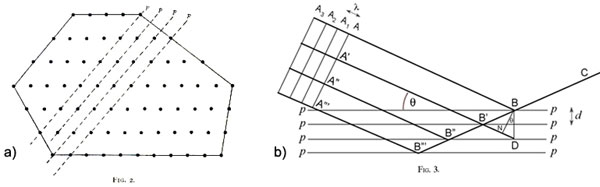
Slika 5.8.
a) Atomi u kristalima leže u ravninama P paralelnim s plohama kristala.
b) Razmak
d između ravnina P
je stalan. Valovi
rendgenskih zraka, A, A', A", A'", koji
padaju na ravnine P "reflektiraju"
se pod kutom θ u točkama, B, B', B'',
B''' te konstruktivnom
interferencijom daju zraku C.
Izvor: http://www.archive.org/stream/xrayscrystalstru00braguoft#page/16/mode/2up
Braggova
jednadžba, nλ = 2dhkl
sinθ, povezuje
razmak dhkl
između
susjednih mrežnih ravnina skupa (hkl)
u kristalu i kut pod kojim se difraktiraju rendgenske zrake. Braggov zakon najčešće se objašnjava
sljedećom shemom:
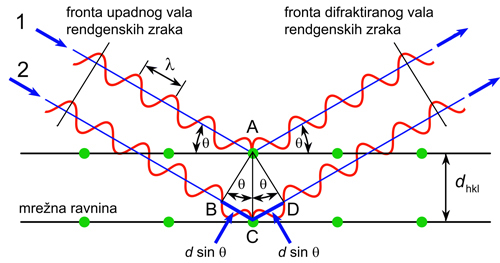
Slika 5.9. Dvije paralelne zrake 1 i 2 upadaju na skup mrežnih ravnina kristala pod kutom θ. Razmak između mrežnih ravnina je dhkl. Zraka 2 prijeđe dulji put od zrake 1 i to za BC + CD. Kad je razlika duljine puta jednaka cjelobrojnom višekratniku valne duljine upadnih zraka, “reflektirane” su zrake u fazi pa dolazi do konstruktivne interferencije. Kut “refleksije” tad je jednak upadnom kutu. Naravno, refleksije nema. To je samo najjednostavniji opis difrakcije rendgenskih zraka na mrežnim ravninama zaposjednutih atomima.
5.4.1.
Braggov difraktometar
William
Henry Bragg (otac) u međuvremenu je preinačio Kirchhoffov
spektroskop. Uzak snop rendgenskih zraka padao je na plohu (100)
kristala
natrijeva klorida na rotirajućem stoliću na mjestu gdje se inače
nalazila
prizma. Okular je zamijenio ionizacijskom komorom. Zrake "reflektirane"
kristalom ulaze u ionizacijsku komoru i ioniziraju plin u komori (SO2).
Zbog ionizacije kroz komoru poteče električna struja razmjerna
intenzitetu "reflektiranih"
rendgenskih zraka. Istodobnim zakretanjem kristala za kut θ i
detektora (ionizacijske komore) za kut 2θ mogao se odrediti kut "refleksije"
rendgenskih zraka. Kad se snop rendgenskih zraka "reflektira" od
skupa mrežnih ravnina paralelnih
plohi
(100) kristala natrijeva klorida, maksimalna struja opaža se pri
kutovima 5,9o,
11,85o i 18,15o. Sinusi
tih kutova su 0,103, 0,205 i
0,312. Očito je da se sinusi tih kutova nalaze u omjeru 1: 2: 3.
Opaženi maksimumi
struje predstavljaju "refleksije" prvoga, drugoga i trećega reda (n = 1, 2, 3) a
njihov omjer potvrđuje ispravnost Braggove
jednadžbe nλ = 2d sinθ.
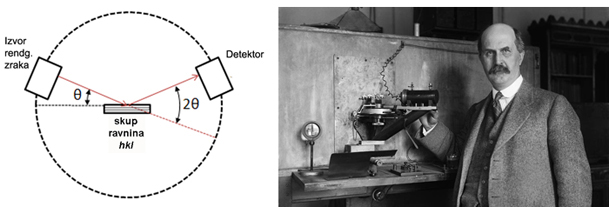
Slika
5.10.
a) Shematski prikaz Braggovog difraktometra. Nepomičan Izvor
rendgenskih zraka,
kristal i ionizacijska komora nalaze se u istoj ravnini. Kristal i
detektor
okreću se neovisno jedan o drugome oko iste osovine. Kristal se mora
orijentirati tako da je osovina, oko koje rotiraju kristal i detektor,
paralelna
skupu mrežnih ravnina (hkl) i okomita na ravninu slike. U tom će
slučaju i "reflektirane"
zrake biti u ravnini s detektorom. b) Sir William Henry Bragg kraj svog
difraktometra s ionizacijskom komorom. Slika
izvor:
https://www.telegraph.co.uk/only-in-britain/william-henry-bragg-born/
Iz
Braggove jednadžbe, nλ = 2d sinθ, za određenu valnu duljinu rendgenskih
zraka proizlazi da kut θ pod kojim
se opažaju difrakcijski maksimumi ovisi o razmaku između mrežnih
ravnina dhkl.
Taj razmak ovisi pak o duljinama
perioda kristalne
rešetke a, b,
c pa se dhkl
računa prema sljedećim formulama:

Pojedine
mrežne ravnine imaju različitu orijentaciju u odnosu na
kristalografske osi. Da bi detektor Braggova difraktometra registrirao
difrakcijski maksimum, kristal treba namjestiti tako da os oko koje
rotiraju
kristal i detektor leži u odabranoj ravnini (hkl).
Pri
određivanju kristalnih struktura halogenida alkalijskih metala te
sfalerita ZnS, fluorita CaF2 i pirita FeS2,
W.L. Bragg
mjerio je kutove i intenzitete “refleksa” od mrežnih ravnina paralelnih
s
kristalnim plohama (100), (110) i (111).
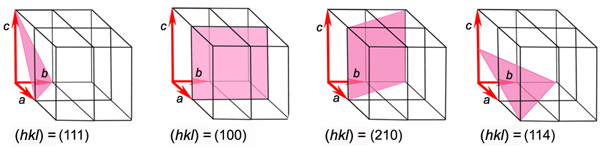
Slika 5.11.
Orijentacija jedne od mrežnih ravnina skupova (hkl) u odnosu na
kristalografske
osi. Susjedna ravnina skupa prolazi ishodištem.
5.4.2.
Struktura natrijeva klorida
Godine
1912. i 1913. tandem otac i sin Bragg istodobno su istraživali
strukturu kristala i analizirali rendgenske zrake. Na temelju Lauevih
difrakcijskih
slika (lauegrama) dobivenih polikromatskim zračenjem, W.L. Bragg
predložio je
kristalnu strukturu NaCl i drugih alkalijskih halogenida. Kasnije je
istu
strukturu, kao i strukture KCl, KBr, ZnS, CaF2,
FeS2,
CaCO3 i neke druge, odredio pomoću očevog "X-Ray
spektrometra"
s monokromatskim zračenjem.

Slika 5.12. a) Kristalna struktura natrijeva klorida, 26.06.1913. b) William Lawrence Bragg. Izvor:
http://rspa.royalsocietypublishing.org/content/royprsa/89/610/248.full.pdf (str. 265)
Spoznaju
da se kristali natrijeva klorida i drugih halogenida
alkalijskih metala sastoje od iona, a ne od molekula, neki su kemičari
primili
s nevjericom. U kristalu natrijeva klorida izmjenjuju se ioni natrija i
klora
tako da je svaki kation na jednakoj udaljenosti okružen sa šest aniona
i
obrnuto. Pritom ione na okupu održavaju samo elektrostatske privlačne
sile. To
je otkriće značajno utjecalo na daljnji razvoj kemije i razumijevanje
prirode
kemijske veze te uzrokovalo rođenje nove znanosti, rendgenske
strukturne analize.

Slika 5.13. a) Koordinacijski poliedar natrija u natrijevu kloridu. b) Model kristalne strukture natrijeva klorida.
Iste
1913. godine otac i sin Bragg odredili su kristalnu strukturu
dijamanta. Pokazali su da se atomi ugljika nalaze u središtu tetraedra
čije
vrhove također zauzimaju atomi ugljika. Zbog toga cijeli kristal
dijamanta
možemo promatrati kao jednu jedinu molekulu. Time je dokazana
ispravnost van't
Hoffove pretpostavke iz 1874. godine da su kemijske veze između
ugljikovih
atoma i njihovih susjeda usmjerene prema vrhovima tetraedra.
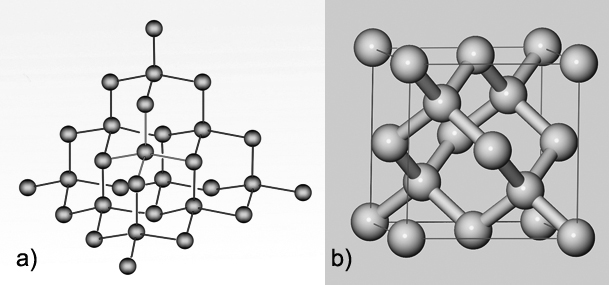
Slika 5.14. a) Shematski prikaz kovalentnih veza između atoma ugljika u dijamantu. b) Jedinična ćelija kristalne strukture dijamanta.
5.4.3.
Valna duljina rendgenskih zraka
Valnu
duljinu rendgenskih zraka moguće je odrediti na temelju Braggove
jednadžbe, nλ = 2d sinθ. Potrebno je samo poznavati razmak
između susjednih mrežnih ravnina i kut "refleksije". Strukturu NaCl
Lawrence
Bragg već je odredio na temelju lauegrama (slika 5.12.a). Kao što se
vidi sa
slike 5.12.a W.L. Bragg za razmak između mrežnih ravnina d200
uzima vrijednost od 2,8 × 10‒8 cm.
Razmak između mrežnih ravnina može se izračunati na osnovi gustoće i
relativne
molekulske mase natrijeva klorida te Avogadrove konstante. Uzmimo
suvremene
podatke za natrijev klorid: M(NaCl)
=
58,44 g mol‒1, ρ(NaCl) =
2,165 g
cm‒3, NA
= 6,022 × 1023 mol‒1.
Jedinična ćelija sadržava 4
formulske jedinke NaCl (natrij: 8 × ⅛ + 6 × ½ = 4,
klor: 1 + 12 × ¼ = 4). Za volumen jedinične
ćelije NaCl dobivamo:
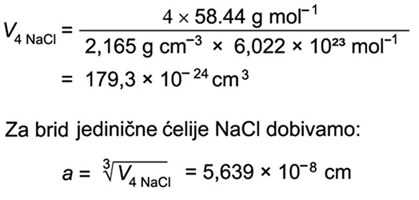
Odavde
proizlazi da je d200
= a/2 = 2,82 × 10‒8 cm.
Za rendgensku cijev s paladijevom anodom "refleks" od skupa mrežnih
ravnina (200) opažen je pri kutu 2θ =
11,7o,
pa sljedi:
λ = 2d
sinθ = 2 × 2,82
× 10‒8 cm × sin 5,85o
= 2 × 2,82
× 10‒8 cm × 0,102 = 0,575
× 10‒8 cm.
Opaska:
W.L.
Bragg je u prvom pokusu koristio tzv. bijelo rendgensko zračenje, a
valna duljina λ = 1,10 ×10‒8
cm odnosila se na najintenzivniju komponentu
upotrijebljenih rendgenskih
zraka. U narednim pokusima koristi zračenje cijevi s paladijevom anodom
(antikatodom) u čijem se spektru javljaju dvije intenzivne linije od
kojih intenzivnija
linija ima valnu duljinu λ = 0,575 ×
10‒8 cm.
Izvori: http://rspa.royalsocietypublishing.org/content/royprsa/89/610/248.full.pdf
http://rspa.royalsocietypublishing.org/content/royprsa/89/613/468.full.pdf
5.5.
Svojstva rendgenskih zraka
Braggov
difraktometar omogućio je tandemu otac i sin Bragg
istraživanje spektra rendgenskih zraka. Istražujući spektre cijevi s
anodama od
različitih metala nedvojbeno su ustanovili da se uz kontinuirano
rendgensko
zračenje javljaju i intenzivne oštre linije karakteristične za metal od
kojega
je načinjena anoda. Pritom su ustanovili da se valna duljina
karakterističnih
linija smanjuje porastom rednog broja elementa upotrijebljenog za
anodu.
Slika 5.15.
Tipičan spektar rendgenskih zraka dobivenih rendgenskom cijevi s
molibdenskom
anodom pri razlici potencijala katode i anode 35 kV. Kα
(λ = 70,9 pm)
i Kβ (λ = 63,2 pm) su
rendgenske zrake čija je
valna duljina karakteristična za molibden.
Izvor: http://www.sliderbase.com/spitem-1106-5.htmle
Naglim
kočenjem elektrona, ubrzanih razlikom potencijala, u metalu
nastaje "bijelo" ili zakočno zračenje (njem. bremsstrahlung)
s kontinuiranim spektrom. Energija emitiranih
fotona ne može biti veća od kinetičke energije, Ekin,
upadnog elektrona. Najmanja valna duljina
rendgenskih zraka izračuna se prema jednadžbi:
Praktičniji
empirijski oblik ove jednadžbe je:
No, dio brzih upadnih elektrona izbija elektrone iz najnižih energijskih nivoa u atomima anode. Ta prazna mjesta popunjavaju elektroni preskokom s viših energijskih nivoa. Pritom se emitiraju rendgenske zrake energije jednake razlici energija tih dvaju nivoa. Tako nastaje tzv. karakteristično rendgensko zračenje.
Slika 5.16. Shematski prikaz nastajanja karakterističnog spektra rendgenskih zraka u cijevima s bakrenom anodom. Izvor: https://en.wikipedia.org/wiki/Siegbahn_notation
Svaki
kemijski element emitira vlastite karakteristične rendgenske
zrake točno određenih valnih duljina, različitih od valnih duljina
drugih
elemenata. Primjerice, anoda od bakra emitira karakteristične
rendgenske zrake Kα1 (λ =
154,05 pm), Kα2 (λ = 154,44 pm),
Kβ (λ = 139,2 pm)
itd. Na tom se temelji rendgenska
spektroskopija. Uzorak se pobudi na emisiju rendgenskih
zraka, a analizom
spektra tih zraka doznaje se elementni sastav uzorka. Curiosity rover kojim se
momentalno istražuje površina Marsa, opremljen je alfa-čestičnim
rendgenskim spektrometrom, APXS, koji uzorke
ozračuje alfa-česticama te bilježi
spektar emitiranih rendgenskih zraka. Analizom tog spektra doznaje se
elementni
sastav stijena na Marsu.
Za rad u
kristalografskom laboratoriju potrebno je rendgensko zračenje
točno poznate valne duljine. To znači da treba ukloniti ili smanjiti
zakočno
zračenje i Kb - zrake. Jedan od načina da bismo to postigli jest
uporaba filtera od tankih metalnih listića. Naime, maseni apsorpcijski
koeficijent
rendgenskih zraka raste porastom valne duljine sve dok je njihova
energija dostatna za izbijanje elektrona iz K-ljuske.
Apsorpcijski koeficijent se skokovito smanji kad energija rendgenskih
zraka
postane manja od one potrebne za izbijanje elektrona iz K-ljuske.
Kao
filter za rendgenske zrake cijevi s bakrenom anodom rabe se
listići od nikla jer apsorpcijski prag za nikal, 148,8 pm, leži između
linija Kα (154,2
pm) i Kβ (139,2
pm). Filter istodobno smanjuje bijelo
zračenje i liniju Kb.

Slika 5.17.
Shematski prikaz djelovanja filtera od nikla na spektar rendgenskih
zraka
cijevi s bakrenom anodom. Općenito, kao filteri rendgenskih zraka rabe
se
listići metala elementa koji u periodnom sustavu elemenata prethodi
elementu na
anodi.
Slika
izvor: http://slideplayer.com/slide/7976813/
Doznajte više
na:
http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/xrayc.html
5.5.1.
Moseleyev
zakon
Već je
rečeno da spektar rendgenskih zraka ovisi o energiji elektrona
i materijalu mete u koju elektroni udaraju. Razlikuju se dvije vrste
spektra.
Kontinuirano ili zakočno zračenje (bremsstrahlung),
odrezano je na kraćim valnim duljinama (λmin)
te ovisi o naponu rendgenske cijevi. Linijski ili karakteristični
spektar ovisi
o materijalu mete, odnosno anode rendgenske cijevi.
Na
temelju Braggovog spektrometra, engleski fizičar Henry Moseley je
1913. godine konstruirao vlastiti vakuumski spektrometar kojim je
istraživao
linijski ili karakteristični spektar rendgenskih zraka. Uočio je da
spektri
svih elemenata imaju jednaku strukturu. Razlikuju se samo valne duljine
karakterističnih linija. One se smanjuju porastom rednog broja elementa
mete.
Moseley je također uočio da je drugi korijen frekvencije
karakterističnih
rendgenskih zraka razmjeran rednom broju elementa mete (Moseleyev
zakon). Tako
je pokazao da atomski ili redni broj, odnosno broj protona u jezgri
atoma,
određuje mjesto elementa u periodnom sustavu elemenata. Ukazao je na
postojanje
još tada neotkrivenih elemenata s rednim brojem 43, 61, 72 i 75.
Također je
dokazao da niz tzv. lantanoida sadržava 14 elemenata. Svojim otkrićima
dao je
značajan doprinos razumijevanju strukture atoma.

Slika 5.18.
a) Karakteristični emisijski spektri rendgenskih zraka nekih elemenata.
b)
Henry Gwyn Jeffreys Moseley (1887. – 1915.) u svom laboratoriju.
Poginuo je 10.08.1915.
u I. Svjetskome ratu na Galipolju - Dardaneli, u jednoj besmislenoj
vojnoj
akciji jednog besmislenog rata. (Dardaneli su morski tjesnac
u
Turskoj
koji
povezuje Mramorno
s Egejskim
morem.)
Doznajte više na: http://www.mysteryofmatter.net/Moseley.html
https://www.youtube.com/watch?v=UTp9jAQpf7c
5.5.2.
Izvori
rendgenskih zraka
Još
u prvoj
polovini 20-og stoljeća kao izvor rendgenskih zraka u medicinske svrhe
rabile
su se Crookesove cijevi s hladnom katodom. No, 1913. godine američki
fizičar i
kemičar William
Coolidge
(1873. – 1975.)
izumio je vakuumsku rendgensku
cijev s volframskom užarenom katodom. Konstrukcija rendgenskih cijevi
od tada
nije se bitno promijenila. Užarena katoda emitira elektrone koji
ubrzani
visokim naponom pri kočenju na anodi uzrokuju emitiranje rendgenskih
zraka. No,
oko 99% energije ubrzanih elektrona pretvara se u toplinu i zato se
anoda hladi
vodom, inače bi se rastalila. Samo oko 1% utrošene energije pretvori se
u
karakteristično rendgensko zračenje. Danas su u upotrebi i mikrofokusne
rendgenske
cijevi i cijevi s anodom od tekućih metala, primjerice galija i indija.
U
kristalografskim istraživanjima rabi se i vrlo snažno rendgensko
zračenje iz
sinkrotrona.
Doznajte više na:
http://bioanalysis.chem.pmf.hr/workshop/X-ray_structure_analysis_workshop_1.pdf

Slika 5.19. a) Shematski prikaz rendgenske cijevi kakva se najčešće rabi u kristalografskim istraživanjima. b) Berilij ima mali apsorpcijski koeficijent za rendgenske zrake i zato se rabi za prozore na rendgenskim cijevima.
6.
Rendgenska strukturna analiza
Strukture jednostavnih binarnih spojeva, koji kristaliziraju u kubnom sustavu, moglo se riješiti na temelju makrosimetrije kristala i mjerenjem intenziteta nekoliko difrakcijskih maksimuma dobivenih od skupova mrežnih ravnina paralelnih s kristalnim plohama (100), (110) i (111).
6.1.
Intenzitet difrakcijskih maksimuma
Rendgenske
zrake su elektromagnetski valovi. Kad se kristal obasja
snopom rendgenskih zraka elektroni u atomima pobude se na vibracije pa
svaki
elektron u pobuđenim atomima postaje izvor novoga kuglastog
elektromagnetskog
vala iste frekvencije, odnosno valne duljine. Kažemo da je došlo do
raspršenja
primarnog snopa. Rendgenske zrake se raspršuju na svim elektronima, pa
intenzitet pojedinog "refleksa" ovisi o broju elektrona u atomima
koji leže u dotičnim mrežnim ravninama. No, intenzitet zraka
difraktiranih na skupu
mrežnih ravnina (hkl) ovisi o nizu
faktora.
Atomski
faktor raspršenja (atomic
scattering factor) proizlazi iz broja elektrona u atomu.
Raste porastom
rednog broja atoma, a smanjuje se s kutom raspršenih zraka te ovisi o
omjeru
sin θ/λ.
Toplinsko
titranje (thermal vibration) atoma
oko ravnotežnog položaja u kristalu čini atom prividno većim. To
uzrokuje
smanjenje atomskog faktora raspršenja razmjerno kvadratu srednje
vrijednosti
amplitude vibracije atoma. Utjecaj toplinskog titranja može se smanjiti
hlađenjem kristala dušikom dobivenim isparavanjem tekućeg dušika.
Strukturni
faktor raspršenja (structure
factor)
uzima
u obzir položaj svih atoma u jediničnoj ćeliji i njihov doprinos
intenzitetu
difrakcijskog maksimuma. Ovisno o položaju u jediničnoj ćeliji pojedini atomi mogu
pridonositi konstruktivnoj ili
destruktivnoj interferenciji. Pokušat ćemo to objasniti na primjeru
"složene" kristalne strukture koja se sastoji od dvije vrsta atoma,
"crvenih" i "crnih", kao što je prikazano na slici 6.1.a.
Uzmimo da se "crni" atomi nalaze u čvorovima primitivne kristalne
rešetke. No, s kojim pravom smo crne atome stavili u ishodište
kristalne
rešetke? "Crveni", "crni" i svaki drugi atom ili točka u
kristalu periodički se ponavljaju u sva tri smjera u prostoru po istoj
zakonitosti. To je smisao kristalne rešetke. Bilo koju kristalnu
strukturu,
koja se sastoji od N atoma, smijemo
razložiti na N jednakih i
paralelnih
kristalnih rešetki koje se međusobno prožimaju.
Ako snop
rendgenskih zraka i kristal dovedemo u takav međusobni
položaj da skup mrežnih ravnina koje čine "crni" atomi zadovoljava
Braggov uvjet, tad i paralelni skup mrežnih ravnina "crvenih" i
svakih drugih atoma zadovoljavaju Braggov uvjet jer se radi o
paralelnim
kristalnim rešetkama i paralelnim skupovima mrežnih ravnina. No, zrake
koje se difraktiraju
u istom smjeru od mrežnih ravnina koje čine "crni" i "crveni"
atomi imaju različite faze. Slika 6.1.b pokazuje da "crvene" mrežne
ravnine premošćuju razmak između "crnih" mrežnih ravnina, i obratno.
Zbog razlike faza intenzitet refleksa od skupa mrežnih ravnina (1-10)
bit će
oslabljen. Sa slike 6.1.c vidimo da "crni" i "crveni" atomi
leže u istim ravninama i difraktiraju s istom fazom. Zato će intenzitet
refleksa od skupa mrežnih ravnina (110) biti pojačan.
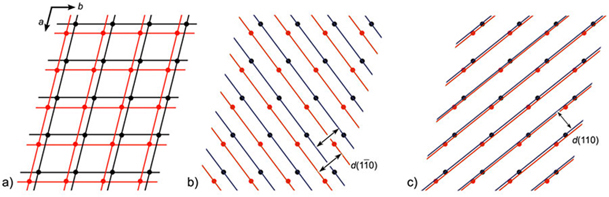
Slika 6.1. a) Shematski prikaz "složene" kristalne strukture koja se sastoji od dvije vrste atoma; "crnih" i "crvenih". b) Difrakcija na "crnim" i "crvenim" skupovima mrežnih ravnina događa se pri istom kutu, ali zbog razlike faza refleks od skupa mrežnih ravnina (1-10) bit će oslabljen. c) "Crni" i "crveni" atomi leže u istim mrežnim ravninama, difraktiraju s istom fazom, pa će refleks od mrežnih ravnina (110) biti pojačan.
Da bismo
bolje razumjeli smisao strukturnog faktora pokažimo to na
konkretnom primjeru kristalne strukture cezijeva klorida čija je
jedinična ćelija
prikazana na slici 6.2. Pretpostavimo da se na vrhovima kocke nalaze
ioni
klora, a u njezinu središtu ioni cezija, ili obratno.

Slika 6.2. Jedinična ćelija kristala cezijeva klorida
Na
Internetu često nailazimo na tvrdnju da je kristalna rešetka
cezijeva klorida prostorno centrirana. No, to nije točno. Kako smo već
objasnili u poglavlju 4.4.1. kristalna rešetka cezijeva klorida je kubna primitivna.
U kubnoj prostorno centriranoj rešetki istovrsni atomi
nalaze se na vrhovima i u središtu kocke, a to ovdje nije slučaj.
Možemo
zamisliti da primitivna rešetka koju čine ioni cezija prodire u
primitivnu
rešetku koju čine ioni klora,
i obratno. Postavlja
se pitanje hoće li se pojaviti refleks 100 zbog razlike faza
rendgenskih zraka
difraktiranih na cezijevoj i kloridnoj primitivnoj rešetki?
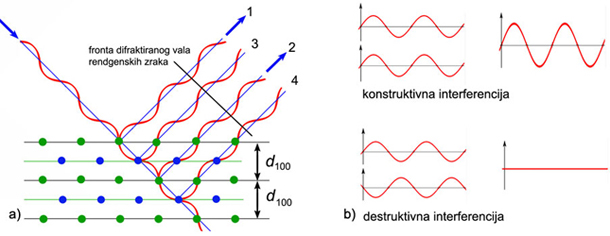
Slika 6.3. a) Shematski prikaz difrakcije rendgenskih zraka u kristalu cezijeva klorida. b) Superpozicijom rendgenskih zraka s istom fazom dolazi do konstruktivne interferencije, odnosno jačanja intenziteta difraktiranog snopa. Ako se faze difraktiranih zraka razlikuju dolazi do destruktivne interferencije, odnosno slabljenja intenziteta difraktiranog snopa.
Sa slike
6.3. vidimo da zrake 1 i 2, koje se difraktiraju na ionima klora
(zeleno), imaju istu fazu. Istodobno
zrake
3 i 4, koje se difraktiraju na ionima cezija (plavo), imaju pomak faze
za 180o
u odnosu na zrake difraktirane na ionima klora. Ion cezija sadržava 54,
a ion
klora 18 elektrona. Zbog destruktivne interferencije intenzitet
refleksa od skupa mrežnih ravnina (100)
odgovarat će recimo intenzitetu kakav bi bio primjeren difrakciji na 54
- 18 =
36 elektrona. Kod primitivne rešetke nema sistematskih pogašenja pa se
pojavljuju svi refleksi.
Zamislimo
da se u ovoj strukturi pojave još i atomi, recimo na položaju
¼¼¼ i ekvivalentnim položajima, tad će i oni svojim brojem
elektrona i fazom difraktiranog vala utjecati na intenzitet svih
refleksa. Svaki val
ima amplitudu koja ovisi o broju elektrona u
atomu i fazu koja ovisi o položaju atoma u jediničnoj
ćeliji. Strukturni
faktor dobije se kao rezultat superpozicije svih valova difraktiranih
na elektronima
u jediničnoj ćeliji.
Ukratko, intenzitet
pojedinog refleksa ovisi o raspodjeli gustoće elektrona i fazama
difraktiranih
valova. Doznajte više na: https://www.iucr.org/__data/assets/pdf_file/0015/13083/3.pdf
http://bioanalysis.chem.pmf.hr/workshop/X-ray_structure_analysis_workshop_1.pdf
Sistematska
pogašenja (systematic absences) refleksa
uvjetovana su simetrijom u kristalu. Ako je kristalna rešetka
primitivna, tad
se javljaju svi refleksi. No, ako je rešetka plošno centrirana, FCC,
kao kod
natrijeva klorida, NaCl, tad se pojavljuju samo refleksi kod kojih su
Millerovi
indeksi ili svi neparni ili svi parni (111, 200, 220, 311, 400, 331,
420), s
tim da su neparni slabijeg intenziteta. Općenito, za plošno
centrirane rešetke (FCC) vrijedi da se refleksi s miješanim
parnim i neparnim indeksima ne pojavljuju.
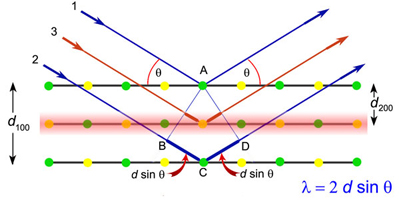
Slika 6.4. Razmještaj iona Na+ i Cl− u skupu mrežnih ravnina paralelnima plohi kocke. Razlika puta zraka 1 i 2 , BCD, jednaka je valnoj duljini rendgenskih zraka, pa bi trebalo doći do konstruktivne interferencije. No, zraka 3 reflektira se na crveno osjenčanoj mrežnoj ravnini, koja sadržava jednak broj elektrona kao i ostale mrežne ravnine, ali je njezina faza pomaknuta za 180o u odnosu na zrake 1 i 2. Zato dolazi do destruktivne interferencije pa se refleks od skupa mrežnih ravnina (100) ne pojavljuje. Naprotiv, pri odgovarajućem kutu θ za skup mrežnih ravnina (200) svi elektroni (ioni) pridonose konstruktivnoj interferenciji pa će zato taj refleks biti jak.
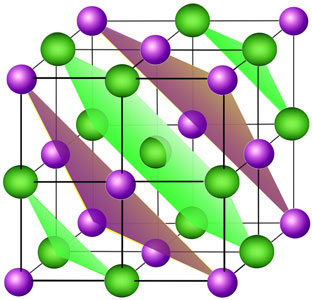
Slika 6.5. Kristalna rešetka natrijeva ili kalijeva klorida. Mrežne ravnine (111), što ih čine klorovi ioni, premoštene su ravninama koje čine natrijevi ili kalijevi ioni. Zbog razlike faza za 180o dolazi do destruktivne interferencije pa je u natrijevu kloridu refleks od skupa mrežnih ravnina (111) oslabljen, a u kalijevu kloridu gotovo se ne pojavljuje. (Vidi poglavlje 7.1.)
Za prostorno centrirane rešetke
(BCC) zbroj Millerovih indeksa uvijek mora biti paran (110, 200, 211,
220, 310,
222 itd.). Na temelju sistematskih pogašenja, osim Bravaisove rešetke,
moguće
je utvrditi prisutnost vijčanih osi, kliznih ravnina i prostornu grupu
(ne baš
uvijek) kojoj kristal pripada.
Osim
kristalne strukture natrijeva klorida, 1913. godine W.L. Bragg je
na osnovi intenziteta "refleksa" od mrežnih ravnina paralelnih s
kristalnim plohama (100), (110) i (111) riješio kristalne strukture
sfalerita,
fluorita i pirita. To su minerali koji bi se trebali nalaziti u svakoj
školskoj
zbirci pa je vrijedno upoznati njihove kristalne strukture.
Sfalerit,
ZnS, je jedan od
prvih kristala na kojima su Laue, Fridrich i Knipping
pokazali difrakciju rendgenskih zraka. Kristalnu strukturu riješio je
W.L. Bragg
1913. godine na temelju rezultata mjerenja na očevom rendgenskom
spektrometru.
Sfalerit kristalizira u kubnom sustavu (a
= 0,543 nm). Kristali sfalerita nemaju centar simetrije. Atomi cinka,
ali i
sumpora, čine plošno centriranu kocku. Njihove rešetke prodiru jedna u
drugu.
Svaki je atom cinka vezan (okružen) s četiri atoma sumpora, i obratno,
svaki je
atom sumpora vezan (okružen) s četiri atoma cinka. Struktura je
analogna (slična)
strukturi dijamanta, ali nije ista. U dijamantu je svaki atom ugljika
vezan s
četiri istovrsna atoma. Kristali dijamanta imaju centar simetrije.
Doznajte više na: http://www.chemtube3d.com/solidstate/_blende(final).htm
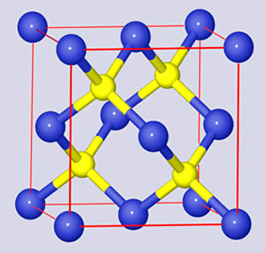
Slika
6.6. Model
kristalne strukture sfalerita, ZnS.
Prirodni
sfalerit je najčešće crn zbog primjesa koje sadržava, ali
može biti i proziran žuto ili crveno obojen. Čisti sfalerit dobiven
sintezom
bijele je boje te se u smjesi s barijevim sulfatom još od 1870-ih rabi
se kao
bijela boja poznata pod imenom litopon.
Cinkov
sulfid važan je poluvodički
materijal
(energijski procijep = 3,54 eV) s izuzetnim fizičkim i kemijskim
svojstvima.
Ima brojne primjene za infracrvene prozore i leće, fotokatalizatore,
senzore UV
svjetla, kemijske senzore (senzori plina), biosenzore i dr. Dopiran
malim
količinama, nekoliko ppm, Ag, Cd, Cu, Mn ili elemenata rijetkih
zemalja,
pokazuje fluorescenciju (ppm = parts per
million - dijelova
na milijun, tj.
jedna čestica primjese na milijun čestica osnovne tvari).
Fluorescenciju
cinkova sulfida opisao je još 1893. Nikola Tesla. Zaslone s premazom
cinkova
sulfida rabili su Rutherford, Röntgen, Laue i mnogi drugi. Katodne
cijevi
crnobijelih televizora imale su premaz od smjese cinkova sulfida
dopiranog
srebrom (ZnS:Ag+) koji fluorescira plavo, i
cinkovog - kadmijevog
sulfida ((Zn,Cd)S:Ag+) koji fluorescira žuto.
Kombinacijom ova dva "fosfora"
dobije se bijela svjetlost.
Doznajte više na: https://www.britannica.com/science/luminescence
https://suw.biblos.pk.edu.pl/downloadResource&mId=1818829
Fluorit,
CaF2,
se pojavljuje u velikim naslagama na mnogim
mjestima širom svijeta. To je industrijski važan mineral. Rabi se za
proizvodnju fluorovodične kiseline, sintezu kriolita
potrebnog
u proizvodnji aluminija, u industriji stakla, keramike, dobivanju
glazura i dr.
Ime fluorit potječe od lat. fluere
-
teći, jer se odavno rabi u metalurgiji kao sredstvo za stvaranje lako
taljive
drozge koja štiti rastaljeni metal od oksidacije.
Čisti
fluorit je bezbojan, ali se zbog različitih primjesa u prirodi
javlja gotovo u svim bojama. Fluorit ima izuzetne optičke
karakteristike,
uključujući nizak indeks loma i nisku disperziju. Propustan je za IR,
VIS i UV
svjetlo. U 1800-tim godinama prirodni kristali kalcijevog fluorida već
se rabe
za leće objektiva u mikroskopima. Danas se sintetički kristali fluorita
rabe za
prozore i leće IR i UV specijalnih uređaja te za leće teleobjektiva
nekih
komercijalnih fotoaparata.

Slika 6.7. Kristal i jedinična ćelija kristalne strukture fluorita
Kristali
fluorita su kubni (a
= 0,546 nm) i najčešće kristaliziraju u obliku kocke i oktaedra. Lako
se kalaju
smjerom ploha oktaedra. Kristalnu strukturu fluorita riješio je 1913.
godine
W.L. Bragg. Rešetka je plošno centrirana. Ioni Ca2+
zauzimaju vrhove
i središta ploha kocke. Osam iona F–
nalazi se
na ¼,¼,¼ i simetrijski ekvivalentnim položajima u jediničnoj
ćeliji. Svaki je ion Ca2+ okružen s 8 iona F–,
koji tvore pravilnu kocku. Istodobno, četiri iona Ca2+
čine pravilan tetraedar u čijem je središtu ion F–.
Doznajte više na: https://www.mindat.org/min-1576.html
Pirit, FeS2, je jedan
od najrasprostranjenijih sulfidnih minerala. Javlja se u obliku
zlatnožutih kubnih
kristala. Poznat je pod imenom lažno zlato ili zlato za budale. U
prošlosti
pirit je bio važan izvor sumpora za dobivanje sumporova dioksida i
sumporne
kiseline. Danas se sumpor dobiva kao nusprodukt pri preradbi nafte i
zemnog
plina. Pirit je poluvodič (energijski procijep = 0,95 eV). Početkom 20.
stoljeća
rabio se kao kristalni
detektor u prvim
radioaparatima.
Pirit
kristalizira u kubnom sustavu (a =
0,542 nm). Kristali pirita često pokazuju “prutanje” što ukazuje
na nižu simetriju u odnosu na simetriju natrijeva klorida i kalcijeva
fluorida.
Kristalnu strukturu pirita odredio je 1913. godine W.L. Bragg.
Znakovito je da
je to ujedno i prvi slučaj primjene Fjodorovih prostornih grupa u
rješavanju kristalne
strukture. U strukturi pirita ioni Fe2+
(narančaste kuglice na slici
6.8.b.) zauzimaju vrhove i središta ploha kocke. No, Bravaisova rešetka
je primitivna.
Svaki je ion Fe2+ okružen sa šest atoma sumpora
koji čine nepravilan
oktaedar.
Slika 6.8. a) Kristal pirita. b) jedinična ćelija kristalne strukture pirita
Položaj
sumpora u strukturi pirita može se izvesti iz strukture
fluorita. U fluoritu 8 iona F– nalazi se
na ¼,¼,¼ i simetrijski ekvivalentnim položajima u jediničnoj
ćeliji. Ako parametar ¼ zamijenimo sa 0,385, atomi sumpora se približe
smjerom prostorne dijagonale kocke pa se dobije struktura kao na slici
6.8. s
disulfidnim ionima, [S-S]2–.
Doznajte više na: http://rruff.geo.arizona.edu/AMS/result.php?mineral=Pyrite
Osim već spomenutih minerala W.L. Bragg je riješio i kristalne strukture natrijeva nitrata, kalcita CaCO3, dolomita CaMg(CO3)2, manganova karbonata i željezova karbonata. Za svoja otkrića otac i sin Bragg dobili su 1915. godine Nobelovu nagradu za fiziku. Lawrence Bragg je najmlađi dobitnik Nobelove nagrade ikada.
6.2.
Eksperimentalni podaci
Nakon što
je W.L. Bragg riješio kristalne strukture natrijeva klorida,
cinkova sulfida, kalcijeva fluorida, natrijeva nitrata i neke druge
jednostavne
kristalne strukture, teorijske osnove difrakcije rendgenskih zraka brzo
su
razrađene. Istodobno su usavršavane filmske kamere, metode određivanja
Millerovih indeksa te metode mjerenja intenziteta difrakcijskih
maksimuma. Za
rješavanje kristalnih struktura složenijih spojeva, koji sadržavaju
više atoma
i koji kristaliziraju u kristalnim sustavima niže simetrije, trebalo je
izmjeriti intenzitete što većeg broja difrakcijskih maksimuma od što
većeg
broja različitih skupova mrežnih ravnina. No, da bi se doznala
struktura, bilo
je potrebno mnogo računanja, i to "pješice". Rješavanje jednostavnije
kristalne strukture, posebno organskih spojeva, moglo je trajati
godinama. Primjerice,
kristalnu strukturu heksametilbenzena, C6(CH3)6,
Kathleen Lonsdale (1903. – 1971.) riješila je 1929. godine, a kristalnu
strukturu heksaklorobenzena, C6Cl6,
dvije godine kasnije.
Tek je rendgenska strukturna analiza pokazala da su sve C-C veze u
aromatskom
prstenu jednake duljine, manje od duljine jednostruke, a veće od
duljine dvostruke
veze. Doznajte više na:
https://skullsinthestars.com/2015/04/06/kathleen-lonsdale-master-of-crystallography/
U
rendgenskoj strukturnoj analizi uvijek se polazi od eksperimenta.
Koji god problem želite riješiti morate najprije naći ili načiniti
dobar
monokristal, veličine 0,1 do 0,4 mm. Zatim slijedi određivanje
kristalnog
sustava i perioda kristalne rešetke te snimanje i mjerenje intenziteta
difrakcijskih maksimuma. No, nećemo objašnjavati kako se to nekad
radilo
filmskim metodama jer tako više nitko ne radi. Revolucija se dogodila
poslije
Drugoga svjetskog rata, tijekom 1960-ih, kad su "kompjutori" postali
dio svakodnevnice. Da bi se detektirao "refleks" od skupa mrežnih
ravnina (hkl) na starom Braggovom
difraktometru kristal se morao orijentirati tako da je os oko koje
rotiraju
kristal i detektor paralelna odabranim ravninama (hkl).
Elektronika i računalne znanosti omogućili su potpunu
automatizaciju tog procesa. Suvremeni automatski rendgenski
difraktometri
sastoje se od tri osnovna elementa (vidi sliku 6.9.): rendgenske cijevi
s
kolimatorom i monokromatorom rendgenskih zraka, držača uzorka na
četverokružnom
goniometru i detektora difraktiranih rendgenskih zraka. Danas je
dovoljno
zalijepiti monokristal na vrh staklene niti, postaviti u centar
difraktometra i
pokrenuti odgovarajući "program" kojim će se prikupiti i izmjeriti
intenziteti
"refleksa" od što većeg broja skupova mrežnih ravnina (hkl).

Slika 6.9. Difraktometar za monokristale u Zavodu za opću i anorgansku kemiju Prirodoslovno-matematičkog fakulteta Sveučilišta u Zagrebu. Kristalić veličine 0,1 do 0,3 mm pomoću četiri računalom upravljana motora dovede se u položaj u kojem pojedini skup mrežnih ravnina (hkl) zadovoljava Braggov uvjet za "refleksiju". CCD detektor omogućuje istodobno mjerenje intenziteta većeg broja "refleksa". Kako radi automatski difraktometar za monokristale doznajte više na adresi: https://serc.carleton.edu/research_education/geochemsheets/techniques/SXD.html
Koliko se "refleksa" može izmjeriti ovisi o parametrima kristalne rešetke, valnoj duljini rendgenskih zraka i kvaliteti kristala. Kristalne strukture "malih molekula" mogu se odrediti na temelju nekoliko stotina ili tisuća "refleksa". Za određivanje kristalnih struktura molekula s većim brojem atoma potrebno je nekoliko desetaka ili stotina tisuća "refleksa". (Pod kristalnom strukturom "malih molekula" misli se na strukture s malim brojem atoma, iona ili molekula u jediničnoj ćeliji.) To je samo početak. Iz podataka dobivenih pomoću difraktometra treba opet odrediti parametre jedinične ćelije i Fjodorovsku prostornu grupu simetrije. Zatim slijedi računanje nekih korekcija, primjerice za polarizaciju i apsorpciju rendgenskih zraka, računanje raspodjele elektronske gustoće u jediničnoj ćeliji, pretpostavljanje te konačno utočnjavanje kristalne strukture. Srećom, kristalografi su razvili niz računalnih programa koji značajno olakšavaju ovaj nekad mukotrpan posao. No, pritom treba dobro poznavati kemiju, jer, oslanjajući se samo na automatiku možete automatski grdno pogriješiti.
6.3.
Raspodjela elektronske gustoće
Sve što
se u rendgenskoj strukturnoj analizi radi ima za cilj odrediti
raspodjelu gustoće elektrona u jediničnoj ćeliji kristala. Već smo
kazali da pri
obasjavanju kristala rendgenskim zrakama određene valne duljine,
primjerice CuKα,
svaki
elektron u kristalu postaje izvor novog kuglastog elektromagnetskog
vala iste
valne duljine. Difrakcijska "slika" je u biti Fourierova transformacija
elektronske gustoće. Zbog periodičnosti kristalne strukture elektronska
gustoća
je periodična funkcija s periodima a,
b i c
u smjeru pojedinih osi. Stoga ju možemo razviti u trodimenzijski Fourierov red, odnosno napisati kao zbroj
jednostavnih trigonometrijskih funkcija, sinusa i kosinusa različitih amplituda, faza i frekvencija.
No, to su već problemi i pitanja
za veliku školu kristalografije, pa se njima nećemo zamarati.
Da bismo
riješili kristalnu strukturu moramo pomoću izmjerenih
intenziteta detektiranih "refleksa"
odrediti točke s maksimalnom elektronskom gustoćom u
jediničnoj ćeliji.
To možemo učiniti obrnutim postupkom, Fourierovom
sintezom. Svaki "refleks" odgovara valu koji se sastoji od
amplitude i faze. Amplituda se može izračunati kao drugi korijen iz
intenziteta
refleksa, ali detektor ne može registrirati fazu i zato je ona
izgubljena. No,
faze sadržavaju bitne informacije za određivanje raspodjele gustoće
elektrona u
kristalu. Razvijeno je više metoda "pogađanja" početnih faza koje se
kasnije mogu utočnjivati. Najviše se rabe tzv. direktne
metode koje se temelje na činjenici da gustoća elektrona u
kristalu ne može biti negativna. Tu metodu često nazivaju "crnom
kutijom" jer se sve odvija automatski putem računala. Od nekoliko
"prijedloga" dobivenih direktnim metodama treba odabrati
najvjerojatniji i pokušati izračunati raspodjelu elektronske gustoće u
jediničnoj
ćeliji. No, i taj je proces također automatiziran. Za rješavanje
kristalnih
struktura malih molekula najčešće se rabi (besplatan) program SHELX
koji je
razvio britanski kemičar George Michael Sheldrick (1942. –).
Od 1978. do
umirovljenja 2011. godine bio je profesor na Sveučilištu
u Göttingenu.
Ukratko, na temelju izračunane
raspodjele elektronske gustoće pretpostavlja se koji se atom nalazi na
nekom
mjestu u jediničnoj ćeliji, a povezivanjem atoma pretpostavlja se
struktura (građa)
molekule. Na osnovi pretpostavljene strukture izračunaju se intenziteti
difrakcijskih maksimuma. Kad se vrijednosti opaženih i izračunanih
intenziteta
difrakcijskih maksimuma dobro slažu, smatra se da je kristalna
struktura istraživanog
spoja riješena. Slika 6.10. prikazuje raspodjelu elektronske gustoće
oko iona
kobalta u molekuli vitamina B12, kao i strukturnu formulu vitamina B12.
Ion
kobalta ima ključnu ulogu u biološkoj aktivnosti vitamina B12.
Slika 6.10. a) Raspodjela elektronske gustoće u korinskom prstenu koji čini jezgru vitamina B12. Strukturu vitamina B12 riješila je 1955. godine Dorothy Hodgkin sa suradnicima. b) Strukturna formula vitamina B12. Uočite korinski prsten koji čine 4 međusobno povezana reducirana pirolna prstena u čijem je središtu atom kobalta. Pažljivo usporedite raspodjelu elektronske gustoće i strukturu korinskog prstena. U mapu raspodjele elektronske gustoće unesite simbole atoma i ucrtajte pripadne jednostruke i dvostruke veze.
Izvori:
http://www.scs.illinois.edu/xray_exhibit/ImagePages/hodkinImage1170.php
https://en.wikipedia.org/wiki/Dorothy_Hodgkin
https://www.mdpi.com/2072-6643/6/5/1861/htm
Slika 6.11. Dorothy Hodgkin (1910. - 1994.) bila je od 1966. dopisna članica JAZU (danas HAZU). Prigodom primanja počasnog doktorata Sveučilišta u Zagrebu, 1969. godine, održala je i predavanje o strukturi vitamina B12.
7.
Debye-Scherrer-Hull-ova metoda
Difrakcija rendgenskih zraka u polikristalnom
uzorku jedna je od najrasprostranjenijih
tehnika u kristalografiji. Rabi
se u različitim područjima kao što
su kemija, fizika, mineralogija, metalurgija, znanost o materijalima,
biotehnologija, biomedicina, ekologija i dr.
Rabi se za
identifikaciju i karakterizaciju spojeva, minerala i njihovih smjesa,
za identifikaciju
faza u geologiji, metalurgiji, kemijskoj tehnologiji, proizvodnji
građevinskih
materijala, kriminalističkim istraživanjima i drugdje.
Prvu difrakciju rendgenskih zraka u
polikristalnim uzorku litijeva fluorida izveo je 1915./1916. Paul
Scherrer pod
vodstvom Petera W. Debyea na Sveučilištu u Göttingenu u Njemačkoj. Za potrebe
snimanja difrakcijske slike kristalnoga
praha Scherrer je načinio filmsku kameru u obliku valjka promjera 57 mm. Prvi rad o
difrakciji rendgenskih zraka u polikristalnom uzorku litijeva fluorida
objavljen
je u časopisu Physikalische
Zeitschrift 28. svibnja 1916. Manje je
poznat rad što ga je u prvom broju Physical
Review 1917. objavio Albert W. Hull iz istraživačkog
laboratorija kompanije General Electric.
Peter Debye (1884. – 1966.) bio je prvi asistent A. Sommerfelda
u Münchenu, a potom profesor na sveučilištima u Zürichu, Utrechtu i
Groningenu.
Paul Scherrer (1890. – 1969.) je pod vodstvom Debyea radio na
svojoj disertaciji. Od 1920. bio je profesor eksperimentalne fizike, a
od 1927.
ravnatelj instituta za fiziku na ETH, Zürich, Švicarska.
Albert Wallace Hull (1880. – 1966.) je u početku bio profesor na Worcester
Polytechnic Institute prije nego što se 1914. godine
pridružio istraživačkom
laboratoriju General Electric Company.
Krajem 1914. godine William Henry Bragg
prihvatio je pozivnicu za dolazak u SAD i Kanadu kako bi održao
nekoliko
predavanja te posjetio Sveučilište Harvard i istraživačke laboratorije General Electric Company. Tom je prilikom
A.W. Hull upitao W.H. Bragga
jesu li odredili kristalnu strukturu željeza. Ne, pokušali smo, ali
nismo uspjeli, odgovorio je W.H. Bragg. U tom odgovoru
Hull je uočio izazov
pa je odlučio pokušati odrediti kristalnu strukturu
željeza. No, nije
imao monokristal pa je nekoliko idućih godina svoju pozornost usmjerio
na
difrakciju rendgenskih zraka u uzorcima kristalnoga praha te odredio
kristalne
strukture 26 elemenata. Za određivanje kristalne strukture željeza Hull
je
upotrijebio prah dobiven redukcijom željezova oksida vodikom. O
kristalnoj
strukturi željeza Hull je izvijestio u listopadu 1916. na 84. sastanku
Američkog fizičkog društva. Rad je objavljen u prvom
broju Physical Review 1917. Tako
se gotovo istodobno u Europi i SAD-u razvilo istraživanje uzoraka
kristalnoga
praha metodom difrakcije rendgenskih zraka.
Doznajte
više na:
http://www.iste.co.uk/data/doc_fgqkuibukrtb.pdf
https://blog.oup.com/2016/09/x-ray-powder-diffraction-method/
ftp://prelog.chem.pmf.hr/pub/POAK/Praktikum%20anorganske%20k%201%20i%202/difrakcija%20na%20prahu_skripta.pdf
Osnovna
ideja difrakcije rendgenskih zraka u uzorcima kristalnoga
praha temelji se na činjenici da su gotovo sve krutine kristalizirane.
Kristalno stanje krutina je pravilo, dok je amorfno stanje iznimka.
Amorfna su
primjerice stakla i neke plastične mase. Praškasti
uzorak bilo koje kristalne tvari sastoji se od mnoštva različito
orijentiranih
kristalića. Ako se takav uzorak stavi u snop rendgenskih zraka uvijek
će se
naći mnoštvo kristalića koji zadovoljavaju Braggov uvjet za difrakciju. Zbog različite
orijentacije kristalića, koji
zadovoljavaju Braggov uvjet, ne dobije se samo jedan "refleks" kao kod
monokristala, već kontinuirani niz refleksa koji čine stošce s otvorom 4q oko
primarne zrake, kao što pokazuje
slika 7.1. To je osnova takozvane metode kristalnoga praha ili
Debye-Scherrerove
metode.
Slika 7.1. Shematski prikaz difrakcije
rendgenskih zraka u
uzorku kristalnoga praha. Nakon
razvijanja na filmu se
vide linije u obliku luka na mjestima gdje "stošci" difraktiranih
zraka sijeku film. Radi bolje vidljivosti svi stošci rendgenskih zraka
nisu
prikazani.

Slika 7.2. Difrakcijska slika praha
jednog metala koji kristalizira
u kubnom sustavu (FCC).
Filmske tehnike snimanja danas
se rijetko rabe. Umjesto filma za registraciju difrakcijskih maksimuma
rabe se difraktometri
s detektorom koji tok fotona pretvara u razmjerne
električne impulse. Dobiveni podaci o intenzitetu refleksa i
difrakcijskom kutu
obrađuju se "programima" koji
uklanjaju
difrakcijske maksimume Ka2
zračenja, snizuju šum i izračunavaju točan položaj svakog difrakcijskog
maksimuma. Konačan rezultat je "file" (tablica) koji sadržava d-vrijednosti i pripadne intenzitete
difrakcijskih maksimuma. Dobiveni "file" može se koristiti u drugim
programima, primjerice za automatsku kvalitativnu i kvantitativnu
analizu faza
sadržanih u uzorku. Mjerenjem položaja difrakcijskih maksimuma pri
većem kutu 2θ
moguće je točnije
odrediti parametre kristalne
rešetke, što je važno primjerice pri dopiranju poluvodiča, legiranju,
istraživanju topljivosti krutina i sl. Na temelju širine difrakcijskih
maksimuma moguće je Scherrerovom
formulom odrediti
prosječnu veličinu
kristalita (čestica
manjih od ~ 1 mm do
nanočestica), što je važno za
suvremenu nanotehnologiju. Mjerenjem intenziteta određenog hkl "refleksa" iz različitih
smjerova s
metalografskog izbruska dobiju se
"figure"
čije konture ukazuju na usmjerenu
orijentaciju kristalita u
istraživanom uzorku. To je važno znati jer usmjerena
orijentacija kristalita
određuje mehanička svojstva metala, keramika,
kompozita, plastičnih masa i dr. Ovih nekoliko primjera ukazuje na
važnost primjene
kristalografije u suvremenoj tehnologiji koja se temelji na rezultatima
znanstvenih istraživanja.
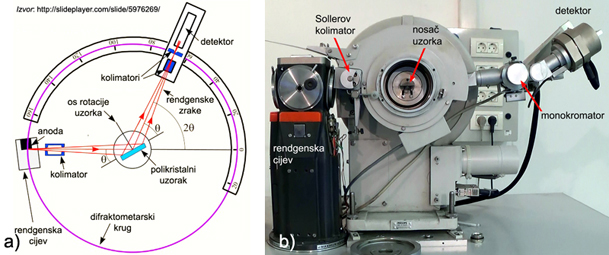
Slika 7.3.
a) Shematski prikaz difraktometra za polikristalne uzorke. b)
Difraktometar za
polikristalne uzorke u Zavodu za opću i anorgansku kemiju PMF-a
Sveučilišta u
Zagrebu.
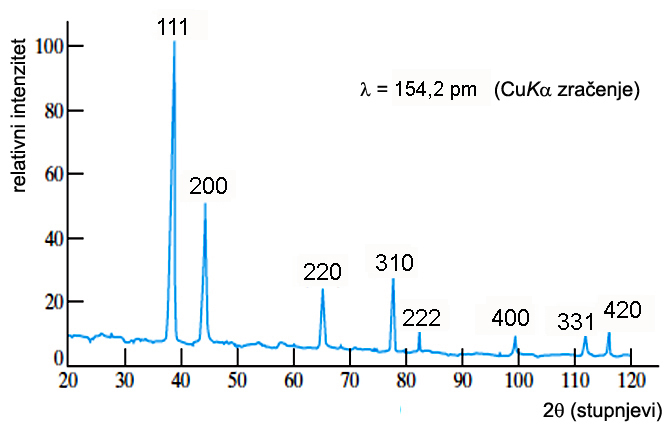
Slika
7.4. Difrakcijska
slika aluminija u prahu snimljena difraktometrom za kristalni prah
Zadatak 7.1.
Na difrakcijskoj slici
aluminija u prahu, prikazanoj na slici 7.4.,
odčitajte vrijednosti kuta 2q za skup mrežnih ravnina (400) i
izračunajte duljinu brida jedinične ćelije aluminija. Aluminij
kristalizira u kubnom
sustavu. Gustoća aluminija je 2700 kg
m–3. Ar(Al)
= 26,98. Koliko
atoma sadržava jedinična
ćelija aluminija?
Rješenje:
Slika 7.5.
Razmak između mrežnih ravnina skupa (400),
d400, jednak je četvrtini perioda kristalne
rešetke.
Iz difrakcijske slike
praha aluminija vidimo da se "refleks" 400
javlja pri kutu 2θ
= 99,4o. Iz Braggove jednadžbe proizlazi:
d400 = λ/2 sinθ = 154,2 pm/(2 sin 49,7o) = 154,2 pm/(2 × 0,7627)
= 101,1
pm
a(Al)
= 4 × d400
= 4 × 101,1
pm = 404 pm = 0,404 × 10–9
m
Broj atoma aluminija u jediničnoj ćeliji
izračunat ćemo tako da masu jedinične ćelije podijelimo masom jednog
atoma
aluminija.
m(ćelije) = V(ćelije)×ρ(Al) = a3×ρ(Al) = (0,404×10–9
m)3×ρ(Al)
= 0,0659×10–27
m3 × 2700 kg m–3 = 178×10–27
kg
Masu jednog atoma aluminija izračunat
ćemo tako da molnu masu aluminija podijelimo Avogadrovom konstantom.
m(atom
Al) = M(Al)/NA
= 26,98 × 10–3
kg mol–1/(6,022 ×
1023
mol–1)
= 44,80
×
10-27 kg
Odavde proizlazi:
Z
= m(ćelije)/m(atom
Al) = 178 × 10–27
kg/44,80 × 10-27
kg
= 4
Doznajte više na:
http://prism.mit.edu/xray/oldsite/Basics%20of%20X-Ray%20Powder%20Diffraction.pdf
http://slideplayer.com/slide/5976269/
7.1.
Identifikacija
kemijskog spoja
Jedna od
najvažnijih primjena difrakcijske slike kristalnoga praha jest
kvalitativna i kvantitativna analiza uzoraka minerala, kemijskih
spojeva,
osobito lijekova, ili smjesa. Različite tvari imaju različit kemijski
sastav i različitu
jediničnu ćeliju kristalne rešetke. Zbog toga se difrakcijske slike
kristalnoga
praha različitih tvari razlikuju. Svaki kristalizirani materijal ima
karakterističnu
difrakcijsku sliku, poput otiska prsta, na temelju kojeg se može
identificirati. Čak je i Curiosity rover (NASA)
opremljen rendgenskim difraktometrom za kristalni prah. Rezultati
analize Marsova
tla pokazuju prisustvo, feldspata,
piroksena
i olivina
te
sugeriraju da je slično tlima nastalim trošenjem bazaltnih stijena
havajskih
vulkana.
Usporedimo
primjerice difrakcijske slike kristalnoga praha natrijeva
klorida i kalijeva klorida. Obje soli imaju jednak razmještaj iona u
kristalu,
odnosno jednaku kubnu kristalnu strukturu, ali im se duljine bridova
jedinične ćelije
razlikuju. Zato se difrakcijske slike kristalnoga praha NaCl i KCl
razlikuju.
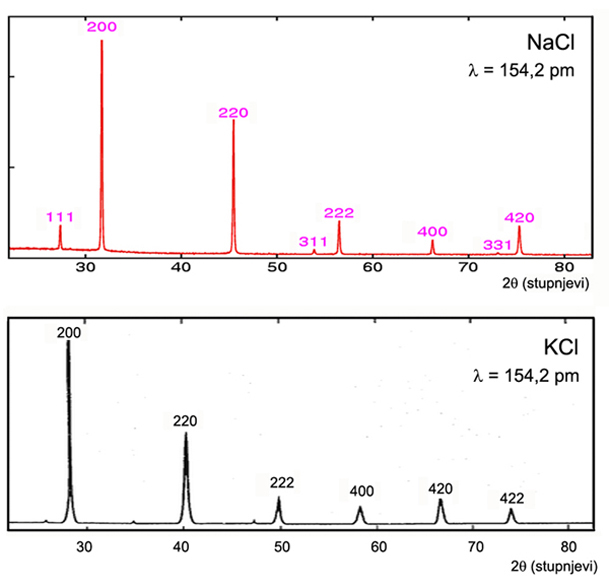
Slika 7.6.
Difrakcijske
slike kristalnoga praha natrijeva i kalijeva klorida. Odčitajte 2q vrijednosti
refleksa
od skupa mrežnih ravnina (400) i izračunajte periode kristalne rešetke
natrijeva
i kalijeva klorida. Koliko formulskih jedinki sadržava jedinična ćelija
ako je ρ(NaCl) = 2160 kg/m³,
a ρ(KCl) = 1980
kg/m³. (Rješenje: a(NaCl)
= 564 pm, a(KCl) = 629
pm. Z = 4.)
Iz
difrakcijskih slika kristalnoga praha možemo uočiti da se kod
natrijeva klorida pojavljuju refleksi sa samo parnim ili samo neparnim
indeksima, pri čemu su refleksi s neparnim indeksima slabijeg
intenziteta. To
je u skladu sa sistematskim pogašenjima karakterističnim za kubnu
plošno
centriranu rešetku, (FCC). No, na difrakcijskoj slici kristalnoga praha
kalijeva klorida pojavljuju se samo refleksi s parnim indeksima, dok su
oni s neparnima
izostali. Tu "anomaliju" možemo objasniti činjenicom da ioni K+
i Cl– imaju po 18
elektrona. Zbog destruktivne interferencije (vidi slike 6.4. i 6.5.)
valova
difraktiranih jednakim brojem elektrona, ali s pomakom faze za 180o,
refleks od skupa mrežnih ravnina (111), kao i drugi refleksi s neparnim
indeksima, neće se
pojaviti na difrakcijskoj
slici kristalnoga
praha kalijeva klorida.
Kemijski
spojevi istoga kemijskog sastava mogu kristalizirati u
različitim kristalnim sustavima i prostornim grupama. Primjerice,
sfalerit i vurcit
imaju isti kemijski sastav, ZnS, ali se njihove difrakcijske slike
kristalnoga praha
drastično razlikuju jer
kristaliziraju u različitim kristalnim sustavima.
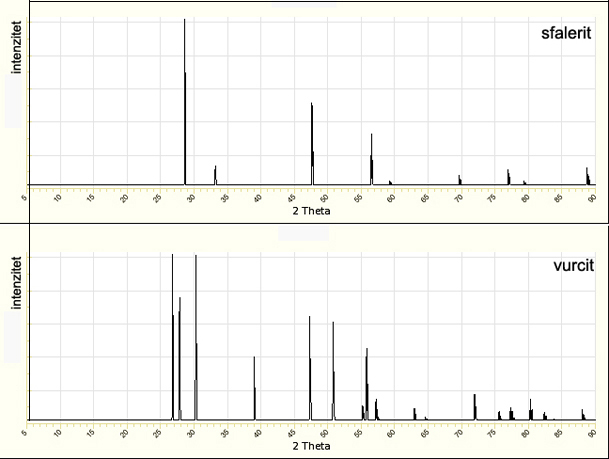
Slika
7.7. Usporedba
difrakcijskih
slika praha sfalerita i vurcita (λ
=154,184
pm).
Izvor: http://rruff.info/Sphalerite/R060636
http://rruff.info/Wurtzite/R060181
Slično je
i s titanijevim dioksidom, TiO2, koji se javlja
u
tri kristalne modifikacije; kao rutil, anatas i brukit. Iako se radi o
istom
kemijskom spoju njihova se fizička svojstva bitno razlikuju.
Primjerice, zbog
specifičnih optičkih svojstava rutil se rabi kao bijeli pigment pri
proizvodnji
boja, papira, plastičnih masa, paste za zube, krema za sunčanje,
kozmetičkih
proizvoda i dr. Anatas i brukit su jeftiniji pa će ih nepošteni trgovci
pomiješati s rutilom i tako ostvariti veću zaradu. Običnom kemijskom
analizom
ne možete uočiti prijevaru, ali će difrakcijska slika kristalnoga praha
za samo
nekoliko minuta pokazati radi li se o čistome rutilu ili smjesi. Više o
upotrebi titanova dioksida doznajte na adresi: http://www.rsc.org/learn-chemistry/resource/res00001268/tio2-photocatalysis-uses-of-titanium-dioxide?cmpid=CMP00002618
Difrakcijske slike kristalnoga praha važno su pomagalo u tehnologiji, znanosti, proizvodnji i identifikaciji lijekova, kriminalistici za identifikaciju droga, kemijskih spojeva ili smjesa. Primjerice, neki lijek može kristalizirati u različiti kristalnim modifikacijama pri čemu je jedna od njih topljivija od druge. Osim kristalne modifikacije kojiput je važna i veličina kristalita koju se može odrediti na osnovi širine difrakcijskih maksimuma.
7.2. Indiciranje
difrakcijskih slika
Od nekih
se tvari ne mogu dobiti kristali pogodni za rendgensku
strukturnu analizu metodom difrakcije u monokristalu. U tom se slučaju
kristalnu strukturu pokušava riješiti iz difrakcijskih slika
kristalnoga praha.
Za rješavanje kristalne strukture iz difrakcijskih slika kristalnoga
praha
ponajprije treba odrediti indekse difrakcijskih maksimuma hkl i parametre jedinične ćelije. Unatoč
suvremenoj tehnologiji
snimanja i moćnim računalima uspjeh u rješavanju kristalne strukture iz
difrakcijskih
slika kristalnoga praha nije zajamčen zbog premalenog broja
"refleksa" koji se dobiju difrakcijom u kristalnom prahu. Nadalje, u
slučajevima
s nižom simetrijom i većim jediničnim ćelijama "refleksi" s različitim
indeksima hkl se prekrivaju pa ih
se
teško razlučuje i ne može se pouzdano odrediti njihov intenzitet. No,
to su već
problemi za veliku školu kristalografije.
Mi ćemo
se u ovom poglavlju pozabaviti s nekoliko primjera indiciranja
difrakcijskih slika kristalnoga praha, određivanja parametara jedinične
ćelije
i tipa kristalne rešetke tvari koje kristaliziraju u kubnom i
tetragonskom sustavu.
7.2.1. Stroncijev titanat
Na slici
7.7. prikazana je difrakcijska slika kristalnoga praha stroncijeva
titanata. Difrakcijski maksimumi obilježeni su slovima od A do I. Cilj
nam je
iz difrakcijske slike odrediti kristalni sustav u kojem stroncijev
titanat
kristalizira, tip kristalne rešetke, Millerove indekse "refleksa" i
periode kristalne rešetke.
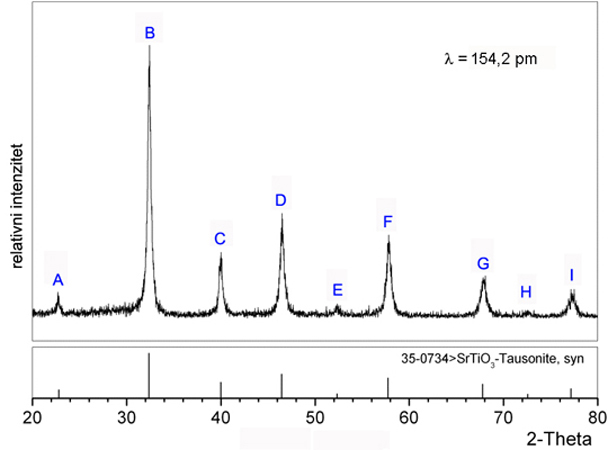
Slika
7.8. Difrakcijska
slika kristalnog praha stroncijeva titanata, SrTiO3.
Izvor: http://electrochemical.asmedigitalcollection.asme.org/article.aspx?articleid=1788214
Za
početak, najbolje je odčitati kutove 2θ
difrakcijskih maksimuma, izračunati
pripadne d-vrijednosti i oformiti
tablicu sa 8 stupaca u koju će se unositi podaci i rezultati
izračunavanja.
Zbog relativno malog broja difrakcijskih maksimuma odmah možemo
pretpostaviti
da stroncijev titanat kristalizira u kubnom sustavu. U tom sustavu
između d-vrijednosti skupova
mrežnih ravnina,
Millerovih indeksa i perioda kristalne rešetke vrijedi sljedeći odnos:
1/d2
= (h2 + k2
+ l2)/a2
gdje je a = period kristalne
rešetke.
Lijeva strana ove jednadžbe mora zadovoljavati Braggovu jednadžbu,
λ = 2d sinθ,
koju ćemo
malo preurediti tako da dobijemo 1/d
= 2 sinθ/λ,
tj.
1/d2 = 4 sin2θ/λ2, pa vrijedi:
4 sin2θ/λ2 =
(h2
+ k2 + l2)/a2
sin2θ/(h2
+ k2 + l2) = λ2/4 a2
Desna
strana jednadžbe sadržava same konstante. Na lijevoj strani
jednadžbe vidimo da su sin2θ vrijednosti
razmjerne zbroju kvadrata Millerovih indeksa. Izračunamo
li pripadne sinθ i sin2θ
vrijednosti opaženih difrakcijskih maksimuma, već na prvi pogled vidimo
da su
sve dobivene vrijednosti sin2θ višekratnici
od vrijednosti dobivene za liniju A. Uzmimo tu vrijednost kao konstantu
K. Podijelimo li izračunane sin2θ vrijednosti
ostalih linija tom konstantom, dobit ćemo zbroj kvadrata Millerovih
indeksa za
svaku pojedinu liniju, (h2
+ k2 + l2), a iz njih
Millerove
indekse refleksa hkl.
Tablica 7.1. Indiciranje difrakcijske slike kristalnoga praha stroncijeva titanata
|
linija |
2θ (o) |
sinθ |
sin2θ |
sin2θ/K |
(h2+k2+l2) |
hkl |
a/pm |
|
A |
22,7 |
0,1968 |
0,0387(K) |
1 |
1 |
100 |
391,8 |
|
B |
32,3 |
0,2782 |
0,0774 |
2 |
2 |
110 |
391,9 |
|
C |
40,0 |
0,3420 |
0,1170 |
3 |
3 |
111 |
|
|
D |
46,4 |
0,3939 |
0,1552 |
4 |
4 |
200 |
|
|
E |
52,3 |
0,4407 |
0,1942 |
5 |
5 |
|
|
|
F |
57,8 |
0,4833 |
0,2336 |
6 |
|
|
|
|
G |
67,8 |
0,5577 |
0,3111 |
|
|
|
|
|
H |
72,6 |
0,5920 |
|
|
|
|
|
|
I |
77,2 |
|
|
|
|
|
|
Parametre jedinične ćelije izračunat ćemo na osnovi jednadžbe:
sin2θ/(h2
+ k2 + l2) = λ2/4 a2
iz koje proizlazi:
a = λ
× (h2
+ k2 + l2)½/2 sinθ
Kako je valna duljina upotrijebljenog zračenja λ = 154,2 pm, dobivamo:
a(A) = 154,2 pm × 1½/(2 × 0,1968) = 391,8 pm
a(B) = 154,2 pm × 2½/(2 × 0,2782) = 391,9 pm
itd ...
Zadatak
7.2.
Popunite
prazna polja u tablici 7.1. Na temelju
rezultata mjerenja zaključite po kojem tipu kristalne rešetke
kristalizira
stroncijev titanat i izračunajte srednju
vrijednost perioda
kristalne rešetke. Može li zbroj kvadrata Millerovih indeksa biti bilo
koji
cijeli broj? Pokažite na primjerima.
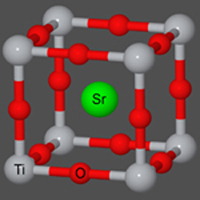
Slika
7.9. Jedinična
ćelija
kristalne strukture stroncijeva titanata, SrTiO3 (mineral:
tausonite). O svojstvima stroncijeva titanata doznajte više na: https://en.wikipedia.org/wiki/Strontium_titanate
7.2.2.
Kalijev bromid
Već smo
kazali da u kubnom sustavu između d-vrijednosti
skupova mrežnih ravnina, Millerovih indeksa i perioda
kristalne rešetke vrijedi sljedeći odnos:
1/d2
= (h2 + k2
+ l2)/a2
gdje je a = period kristalne
rešetke.
Iz
jednadžbe vidimo da su vrijednosti 1/d2
razmjerne zbroju kvadrata Millerovih indeksa. Prema
tome treba naći najmanju razliku između uzastopnih 1/d2
vrijednosti. Uzorak je snimljen pomoću difraktometra
povezanoga s računalom, a podatci obrađeni programom isporučenim
zajedno s
difraktometrom. Upotrijebljeno je CuKα
zračenje, λ =
154,2 pm. Postupak određivanja indeksa vidljiv
je iz tablice 7.2.
Zadatak
7.3.
Popunite
prazna mjesta u tablici 7.2. Po kojem tipu
kristalne rešetke kristalizira kalijev bromid?
Izračunajte srednju vrijednost perioda kristalne rešetke.
Valja
napomenuti da su prve četiri znamenke pouzdane. Peta znamenka već ovisi
o
temperaturi uzorka.
Tablica
7.2. Indiciranje
difrakcijske slike kristalnoga praha kalijeva bromida
|
2 θ |
d/nm |
1/d2 |
diff 1/d2 |
(1/d2)/2,80 |
(h2+k2+l2) |
hkl |
a/nm |
|
25,8099 |
0,3449 |
8,4065 |
|
3.0023 |
3 |
111 |
0,59738 |
|
29,88831 |
0,2987 |
11,208 |
2,8015 |
4.0028 |
4 |
200 |
0,5974 |
|
42,7802 |
0,2112 |
22,4188 |
11,2108 |
8.0067 |
8 |
220 |
0,59736 |
|
50,64283 |
0,1801 |
30,8299 |
8,4111 |
11.0106 |
11 |
311 |
0,59732 |
|
53,04371 |
0,1725 |
33,6064 |
2,7765 |
12.0022 |
12 |
222 |
0,59755 |
|
62,11896 |
0,1493 |
44,8622 |
11,2558 |
16.0222 |
16 |
400 |
|
|
68,42283 |
0,137 |
53,2793 |
8,4172 |
19.0283 |
19 |
|
|
|
70,41747 |
0,1336 |
56,0257 |
2,7463 |
20.0091 |
|
|
|
|
78,38014 |
0,1219 |
67,2965 |
11,2708 |
|
|
|
|
|
84,1946 |
0,1149 |
75,746 |
|
|
|
|
|
|
93,79345 |
0,1055 |
|
|
|
|
|
|
|
99,53137 |
|
|
|
|
|
|
|
7.2.3.
Litij
Litij
kristalizira u kubnom sustavu po tipu prostorno
centrirane rešetke (BCC), što znači da zbroj Millerovih
indeksa difrakcijskih maksimuma mora biti paran. Kao što smo već
pokazali
između kutova pri kojima se pojavljuju difrakcijski maksimumi, perioda
kubne
kristalne rešetke i valne duljine rendgenskog zračenja vrijedi sljedeći
odnos:
sin2θ/(h2
+ k2 + l2)
= λ2/4 a2
pa je
broj "refleksa" ograničen periodom kristalne rešetke
i valnom duljinom rendgenskog
zračenja.
Zadatak
7.4
Litij
kristalizira u kubnom sustavu. Kristalna rešetka
je prostorno centrirana (BCC) te ima period rešetke a
= 351 pm. Izračunajte kutove 2θ
pri kojima se javljaju difrakcijski maksimumi od uzorka metalnog litija
u prahu
uz CuKα
zračenje,
λ = 154,2 pm i MoKα zračenje, λ = 70,9 pm. Obratite
pozornost na sistematska pogašenja za BCC rešetku.
Zadatak
7.5.
Na
slici 7.2. prikazana je difrakcijska slika kristalnoga
praha nekog metala koji kristalizira u kubnom sustavu. Običnim ravnalom
odčitajte
kutove difrakcijskih maksimuma, izračunajte vrijednosti sinq
i sin2θ te
odredite vrijednosti dhkl
i indekse hkl
difrakcijskih maksimuma. Odredite tip Brawaisove kristalne rešetke (P,
BCC ili
FCC). Izračunajte duljinu perioda jednične ćelije. Kad proučite
poglavlje 8. Baze podataka, na
temelju prve tri vrijednosti
dhkl
difrakcijskih
maksimuma ustanovite koji metal daje takvu difrakcijsku sliku.
(Rješenje: Cu)
7.2.4.
ThNi2Si2
Indiciranje
difrakcijske slike kristalnoga praha tvari koje kristaliziraju
u kubnom sustavu relativno je jednostavno i može se izvesti
"pješice". No, stvari postaju kompliciranije već za tetragonski
sustav.
U
tetragonskom sustavu sin2θ
vrijednosti difrakcijskih maksimuma nalaze se u sljedećem
odnosu:
sin2θ =
A
× (h2 + k2)
+ C ×
l2
gdje su A = (λ2/4a2) i C = (λ2/4c2) konstante
specifične za pojedini
uzorak.
Najprije
treba odrediti konstante A i C pomoću kojih se mogu
izračunati parametri jedinične ćelije. Konstanta A dobije se pomoću
"refleksa" s indeksima hk0.
Kad je l = 0 gornja jednadžba
dobiva
oblik:
sin2θ =
A × (h2
+ k2)
Moguće
vrijednosti za (h2
+ k2) su 1,
2, 4, 5, 8,
itd. Stoga linije s indeksima hk0 moraju
imati sin2θ vrijednosti u omjeru ovih cijelih brojeva. To
znači da je konstanta A broj koji je
jednak 1, 1/2, 1/4, 1/5, 1/8,
itd. od sin2θ
vrijednosti linija s indeksima hk0.
Konstanta
C dobije se iz preostalih linija pomoću jednadžbe:
sin2θ ‒
A
× (h2
+ k2) = C × l2
Vrijednosti
C × l2
mogu biti u
omjeru 1, 4, 9, 16 itd, a razlike na lijevoj strani jednadžbe
izračunaju se na
temelju pretpostavljenih vrijednosti h
i k.
Zadatak
7.6.
Na temelju podataka
prikazanih u tablici 7.3. odredite
indekse "refleksa" na difrakcijskoj slici kristalnoga praha
međumetalnog spoja ThNi2Si2
koji kristalizira u tetragonskom sustavu.
Odredite
parametre kristalne rešetke a i c. Difrakcijska slika dobivena je
difraktometrom za kristalni prah pomoću CuKa zračenja, λ
= 154,2 pm.
Rješenje
Prvi
"refleksi" (linije) difrakcijske slike potječu od
mrežnih ravnina s najjednostavnijim indeksima kao što su primjerice:
(001), (100),
(101), (110), (111), (002), (200), (102), (201) itd. U
tablici 7.3. potražite višekratnike sin2q vrijednosti
prvih nekoliko linija. Lako
je uočiti da se sin2θ vrijednosti
linija broj 1, 6 i 23 nalaze u
omjeru 1 : 4 : 16.
Isto tako sin2θ vrijednosti linija 3, 7, 13, 19 i 31
nalaze se
u omjeru 1 : 2 : 4 :
5 : 8. Kako
l2
ne može biti 5, proizlazi da linije 3, 7, 13, 19 i 31 imaju Millerove
indekse hk0, a linije broj 1, 6 i
23 imaju
indekse 00l.
Na
temelju svojstava opaženih sin2θ vrijednosti
treba isprobati nekoliko
pretpostavki. Za linije broj 1,
6 i 23
pretpostavljeni indeksi mogu biti redom: 001, 002,
004 ili 002, 004, 008. Ako linija 23 ima indeks 004 tad je konstanta C
=
0,4163/16 = 0,0260. Ako se pretpostavi da linija 23 ima indeks 008 tad
je
konstanta C = 0,4163/64 = 0,0065.
Za linije 3, 7, 13, 19 i 31 pretpostavljeni indeksi mogu biti redom: 100, 110, 200, 210, 220, ili 110, 200, 220, 310, 400. Ako linija 31 ima indeks 400, tad je konstanta A = 0,5715/16 = 0.0357. Sve preostale linije imaju indekse hkl. Pripadne indekse pojedinih "refleksa" odredite metodom probe i pogreške pomoću jednadžbe sin2θ = A × (h2 + k2) + C × l2.
Tablica 7.3. Indiciranje difrakcijske slike međumetalnog spoja ThNi2Si2
|
Refleks broj |
Relativni intenzitet |
sin2θopaženo |
Višekratnici sin2θ |
sin2θ = A×(h2
+ k2) + C×l2 |
hkl |
|
1 |
17 |
0,0261 |
0,0261
(1) |
0,0065 × 4 = 0,0260 |
002 |
|
2 |
160 |
0,0432 |
|
0,0357 + 0,0065 = 0,0422 |
101 |
|
3 |
34 |
0,0716 |
0,0716
(1) |
2 × 0,0357 = 0,0714 |
110 |
|
4 |
115 |
0,0945 |
|
0,0357 + 9 × 0,065 = 0,0942 |
103 |
|
5 |
200 |
0,0976 |
|
2 × 0,0357 + 4 × 0,0065 = 0,0974 |
112 |
|
6 |
30 |
0,1043 |
0,1043
(4) |
16 × 0,0065 = 0,1040 |
004 |
|
7 |
70 |
0,1430 |
0,1430
(2) |
4 × 0,0357 = 0.1428 |
200 |
|
8 |
11 |
0,1689 |
|
4 × 0,0357 + 4 × 0,0065 = 0,1688 |
202 |
|
9 |
46 |
0,1853 |
|
5 × 0,0357 + 0,0065 = 0,1850 |
211 |
|
10 |
40 |
0,1985 |
|
|
|
|
11 |
65 |
0,2373 |
|
|
|
|
12 |
30 |
0,2471 |
|
|
|
|
13 |
28 |
0,2855 |
0,2855 |
|
|
|
14 |
33 |
0,3058 |
|
|
|
|
15 |
5,3 |
0,3119 |
|
|
|
|
16 |
10 |
0,3280 |
|
|
|
|
17 |
33 |
0,3410 |
|
|
|
|
18 |
7 |
0,3546 |
|
|
|
|
19 |
14 |
0,3570 |
0,3570 |
|
|
|
20 |
14 |
0,3797 |
|
|
|
|
21 |
35 |
0,3829 |
|
|
|
|
22 |
14 |
0,3897 |
|
|
|
|
23 |
5,8 |
0,4163 |
0,4163
|
|
008 |
|
24 |
9,8 |
0,4709 |
|
|
|
|
25 |
9,1 |
0,4839 |
|
|
|
|
26 |
7,0 |
0,4878 |
|
|
|
|
27 |
9,3 |
0,4974 |
|
|
|
|
28 |
5,0 |
0,5199 |
|
|
|
|
29 |
15 |
0,5228 |
|
|
|
|
30 |
14 |
0,5594 |
|
|
|
|
31 |
7,0 |
0,5715 |
0,5715 (8) |
|
400 |
|
32 |
28 |
0,5913 |
|
|
|
|
33 |
9,3 |
0,6137 |
|
|
|
Parametar
a kristalne
rešetke može se izračunat pomoću konstante A.
A = λ2/4a2
Odavde
proizlazi
a2
= λ2/4A
= (154,2 pm)2/(4×0,0357) =
166 510 pm2
a = 408 pm
Parametar
c kristalne
rešetke može se izračunati pomoću konstante C.
C = (λ2/4c2)
Odavde
proizlazi
c2
= λ2/4C
= (154,2 pm)2/(4×0,0065) =
914 524 pm2
c = 956 pm
Periode
kristalne rešetke a
i c izračunane su na temelju sin2θ vrijednosti
za reflekse 400 i 008. Točnije
vrijednosti perioda rešetke dobiju se kad se u izračunu koriste sin2θ vrijednosti
svih opaženih refleksa, kao što je
to učinjeno u radu: Z. Ban and M. Sikirica, The
Crystal Structure of Ternary Silicides ThM2Si2
(M =
Cr, Mn, Fe, Co, Ni and Cu), Acta Cryst.
(1965) 18, 594 - 599. Rad je
dostupan na adresi: https://journals.iucr.org/q/issues/1965/04/00/a04587/a04587.pdf
Slika
7.10.
Kristalna struktura međumetalnih spojeva tipa ThM2Si2.
Postupak određivanja kristalne
strukture
na temelju dobivene difrakcijske slike pripada velikoj školi
kristalografije,
pa se time nećemo zamarati.
Danas je
poznato nekoliko stotina međumetalnih spojeva strukturnoga
tipa ThM2Si2. Uz
suvremene difraktometre i pripadne
"programe" za rješavanje i utočnjavanje ovakvih i sličnih
jednostavnih kristalnih struktura potrebno je nekoliko sati. No, 1963.
godine, kad su otkrivene i rješavane prve kristalne strukture tipa ThM2Si2,
nije bilo računala pa je trebalo utrošiti puno vremena i papira kako bi
se
"pješice" doznala i utočnila njihova kristalna struktura.
Sve objavljene difrakcijske slike poznatih tvari skupljene su u International Centre for Diffraction Data, Pennsylvania, USA. Uspoređivanjem difrakcijskih slika kristalnoga praha poznatih spojeva i difrakcijske slike nepoznatog uzorka može se identificirati element, slitina, spoj ili smjesa spojeva. Za to su dostatne dhkl vrijednosti triju najintenzivnijih linija difrakcijske slike kristalnoga praha. Suvremeni računalni programi pomažu nam da dobivene difrakcijske slike kristalnoga praha odmah usporedimo s bazom podataka, identificiramo spoj ili fazu te dobijemo druge korisne informacije kao što su literaturne reference.
8.
Baze podataka
Svaka
škola, naselje ili grad danas ima svoju knjižnicu. Ideja
knjižnice naslijeđe je staro nekoliko tisuća godina. Već oko 700. pr.
Kr. narodi Mezopotamije imali su
uređene knjižnice po svojim hramovima i palačama. "Knjige" u tim
knjižnicama bile su glinene pločice ispisane klinastim pismom. Tisuće takvih pločica raspoređenih prema
područjima znanosti, činile su
zbirke koje su predstavljale prve prave knjižnice. Jedna od takvih
zbirki, tzv.
Asurbanipalova
knjižnica s oko
22.000 glinenih pločica, danas se čuva u British Museum u Londonu. Egipćani su također
imali knjižnice s knjigama u obliku svitaka od papirusa. Najpoznatija
knjižnica
svih vremena, Aleksandrijska
knjižnica, osnovana
je 300. pr.
Kr. Procjenjuje
se da je sadržavala 500 000 do 700 000 svitaka papirusa. Knjižnica
nije bila otvorena za javnost nego samo za studente i znanstvenike.
Današnji
studenti i znanstvenici ne moraju više sjediti u knjižnicama
jer su svi znanstveni časopisi i baze podataka dostupni "on line".
Naime, nekada su važan izvor informacija bili znanstveni časopisi u
tiskanom
izdanju. No, tijekom vremena broj znanstvenih časopisa i objavljenih
radova počeo
se toliko povećavati da je nastala potreba stvaranja baza podataka. U
svakom znanstvenom
području znanstvenici su izgradili ili grade i stalno nadopunjuju
prikladne baze
podataka. Računala, pa čak i mobiteli, omogućuju nam
da u svakom trenutku s bilo kojeg mjesta
pronađemo i dobijemo traženi podatak,
informaciju ili znanstvenu publikaciju. U ovom ćemo
poglavlju spomenuti
samo neke baze podataka koje su u najužoj vezi s kristalografijom.
Doznajte
više na adresi:
https://www.chemistry.mcmaster.ca/~xman/cccw17/files/CCCW16-Databases-Sarjeant.pdf
8.1.
Kemija
Prvi
korak u stvaranju baze podataka u kemiji napravio je Leopold Gmelin (1788. – 1853.)
kad je 1817. u Frankfurtu na Majni počeo objavljivati Handbuch
der Theoretischen Chemie. U to doba nije još postojala
podjela na organsku i anorgansku kemiju. No, uskoro se broj podataka
toliko
povećao da je od petog izdanja, objavljenog 1852. – 1853., sadržaj
ograničen
samo na anorganske spojeve. Tako je nastao Gmelin´s
Handbuch der Anorganischen Chemie, čije je tiskano izdanje
prestalo
izlaziti 1997. godine. U 116 godina izlaženja objavljeno je 760 svezaka
s oko
240 000 stranica. Friedrich Konrad Beilstein
(1838. –
1906.), ruski kemičar njemačkog podrijetla, još je od studentskih dana
bilježio
rezultate istraživanja iz područja organske kemije te je 1881. godine
objavio
čuveni Handbuch der organischen Chemie.
Prvo izdanje ovog priručnika obuhvatilo je podatke o 1.500 spojeva na
2.200
stranica.
Ovaj priručnik sada je poznat
kao Beilsteinova
baza podataka. To je
najveća baza
podataka u području organske
kemije, u kojoj je
obuhvaćena znanstvena literatura od 1771. do danas.
Sadržava podatke o oko 7 milijuna kemijskih
reakcija i tvari, preuzete
iz izvornih znanstvenih
publikacija. Danas
su Gmelin´s Handbuch der Anorganischen Chemie
i Handbuch der organischen Chemie
uključeni u bazu podataka Reaxys, Elsevier.
Kristalografima je najvažnija The Cambridge
Structural Database (CSD)
utemeljena 1965. godine. Ona
sadržava podatke za preko 1 000 000 riješenih kristalnih struktura. Svaki
unos obogaćen je bibliografskim podacima te podacima o kemijskim i
fizičkim
svojstvima spoja, što dodatno pridonosi vrijednosti sirovih strukturnih
podataka.
Rad s CSD
bazom je jednostavan. Primjerice, kliknite na https://www.ccdc.cam.ac.uk/structures/ i u
rubriku Compound
name upišite DDT,
što je sinonim za
1,1-bis(p-Chlorophenyl)-2,2,2-trichloroethane, nekad popularni
insekticid.
Dobit ćete podatke o parametrima jedinične ćelije. Klikom na Database Identifier CPTCET10 otvorit će se novi
ekran s prikazom
strukturne formule, literaturnim i drugim podacima te modelom molekule.
Model
rotira i možete ga zaustaviti u odabranom položaju. U izborniku (Menu) odaberite primjerice: File / Export / Export JPG image.
Dobivenu sliku otvorite i spremite u svoju datoteku. Ako odaberete
opciju Export POV-Ray image pojavit
će se Jmol.pov file. Otvaranjem tog
file-a
dobit ćete renderiranu sliku
molekule DDT-a kakva je prikazana na slici 8.1. Sami istražite ostale
mogućnosti koje vam pruža CSD baza podataka.

Slika 8.1. Model molekule DDT-a, nekad popularnog insekticida, generiran CSD bazom podataka.
Pokušajmo
pretragu CSD-a još jednom s imenom osnivača rendgenske
strukturne analize u Hrvatskoj, akademika Draga Grdenića. U rubriku Authors upišite D.
Grdenic i kliknite na Search.
Pojavit će se popis s više od 30 publikacija. Kliknite, na primjer, na Database Identifier AXHGME20 pa će se otvoriti
novi ekran s
kristalografskim podacima, strukturnom formulom i modelom molekule. U
izborniku
(Menu) odaberite File
/ Export / Export
POV-Ray image. Pojavit će se Jmol.pov
file. Otvaranjem tog file-a dobit ćete renderiranu sliku,
ovdje prikazanu kao slika 8.2.

Slika 8.2. Tetrakis(Acetoxy-mercury)methane dihydrate. Izvor: Grdenić, D.; Sikirica, M.: Die Kristallstruktur von Tetrakis(acetoxyquecksilber)methan-Dihydrat, Z. Kristallogr. 150 (1979) 107-114
Ako vas zanimaju radovi drugih kristalografa upišite njiihovo ime u rubriku Authors i kliknite na Search. O CSD bazi podataka doznajte više na adresi: https://journals.iucr.org/j/issues/2010/05/02/kk5063/index.html
8.2.
Mineralogija
Mineralozima
je na raspolaganju predivna "on line" baza
podataka dostupna na adresi: http://webmineral.com/ Ova baza
obuhvaća podatke o 4714 minerala. Ako mineralogija ili kristalografija
nije vaš
primarni interes, ipak je vrijedno pročeprkati po ovoj bazi i pogledati
samo
slike minerala. Možete doznati kemijski sastav, parametre jedinične
ćelije,
kristalnu strukturu, difrakcijsku sliku kristalnoga praha, fizička i
optička
svojstva minerala poredanih po nazivima abecednim redom. Na osnovi dhkl vrijednosti tri najintenzivnije linije difrakcijske
slike kristalnoga praha možete i identificirati svoj mineral. Baza uključuje mnoštvo
poveznica na vanjske
izvore informacija i software. Osim toga, ova baza nije samo baza
podataka već
i udžbenik kristalografije.
Nekim
mineralozima zanimljivija je
American Mineralogist Crystal Structure Data Base dostupna na
adresi: http://rruff.geo.arizona.edu/AMS/amcsd.php. Kliknite
na navedenu adresu i pod Mineral upišite ime
prvog minerala kojeg se sjetite, primjerice olivine, i dobit
ćete sljedeće podatke:
Olivine
Miyake
M, Nakamura H, Kojima H, Marumo F
American
Mineralogist 72 (1987) 594-598
Cation
ordering in Co-Mg olivine
solid-solution series
Sample:
Co18
_database_code_amcsd
0001090
4.780
10.290 5.997 90 90 90 Pbnm
atom
x
y
z
occ U(1,1) U(2,2) U(3,3) U(1,2) U(1,3) U(2,3)
Co1
0
0
0 .928
.0036 .0076 .0072 -.0001 -.0006 -.0011
Mg1
0
0
0 .072
.0036 .0076 .0072 -.0001 -.0006 -.0011
Co2
.9911 .2765
.25 .807 .0050
.0060 .0081
-.0001
0
0
Mg2
.9911 .2765
.25 .193 .0050
.0060 .0081
-.0001
0
0
Si
.4277 .0948
.25
.0027
.0058 .0072 .0002
0
0
O1
.7665 .0921
.25
.0037
.0096 .0088
-.0003
0
0
O2
.2154 .4483
.25 .0053
.0056 .0104 .0003
0
0
O3
.2816 .1641 .0337
.0069 .0088
.0080 .0004
-.0005 .0015
Download
AMC data (View
Text File)
Download
CIF data (View
Text File)
Download
diffraction data (View
Text File)
View
JMOL 3-D Structure (permalink)
Podaci
uključuju imena autora, časopis (volumen, godina stranica),
naslov rada, parametre jedinične ćelije i prostornu grupu. Tablica
sadržava
koordinate atoma i occ, odnosno faktor zaposjednutosti. Naime,
istraživani
uzorak je kruta otopina, pa statistički gledano koordinatu x = 0, y
= 0, z = 0 zaposjeda 0,928 atoma
Co(1) i 0,072
atoma Mg(1). Drugo mjesto s koordinatama x
= 0.9911, y = 0.2765, z = 0.25, zaposjeda 0,807 atoma Co(2) i
0,193 atoma Mg(2). Stupci U(1,1) U(2,2) U(3,3) U(1,2) U(1,3) U(2,3), u
prikazanoj tablici sadržavaju anizotropne temperaturne faktore. Naime,
atomi ne
miruju već titraju oko ravnotežnih položaja, svaki za sebe i u različitim smjerovima u odnosu na
kristalografske osi.
No, to su već pitanja za veliku školu kristalografije.
Klikom na
ikonu
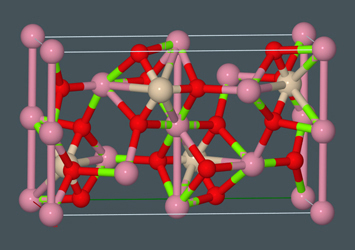
Slika
8.3. Jedinična ćelija
kristalne strukture olivina.
Istražujte
dalje sami ovu bazu podataka. Kliknite na Download
diffraction data (View Text
File) pa
ćete dobiti difrakcijsku sliku kristalnoga
praha olivina. Kliknite na complete
list of
minerals i dobit ćete popis minerala.
Klikom na
odabrani mineral dobivate sve podatke o odabranom mineralu, kao što smo
pokazali na primjeru olivina. Korisno, poučno i zabavno. Ako
nikad
niste imali priliku vidjeti olivin ili neki drugi mineral, tad otvorite Online Mineral
Museum.
Pokušajmo
još jednom pretražiti tu bazu imenom akademika Vladimira
Bermanca, profesora Geološkog odsjeka PMF-a. U rubriku Author
upišite Bermanec.
Otvorit će
vam se popis radova, a na prvom mjestu pokazat će se sljedeći podaci: Tuzlaite, Bermanec V, Armbruster T,
Tibljas D, Sturman D, Kniewald G,
American Mineralogist 79
(1994)
562-569 Tuzlaite,
NaCa[B5O8(OH)2].3H2O,
a new mineral with a pentaborate sheet
structure from the Tuzla salt mine, Bosnia and Hercegovina.
Kliknite na View JMOL 3-D
Structure (permalink) pa
ćete
dobiti sliku jedinične ćelije tuzlaita kao na slici 8.4.
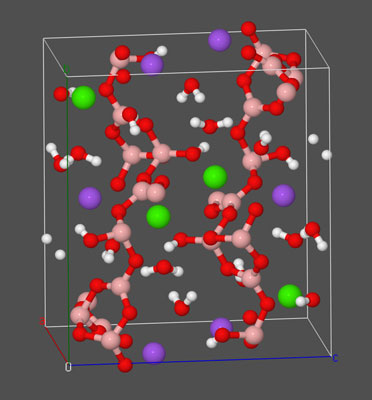
Slika 8.4. Jedinična ćelija kristalne strukture tuzlaita, NaCa[B5O8(OH)2].3H2O,
8.3.
Molekulska biologija
Rendgenska
strukturna analiza primarna je metoda u određivanju
kristalnih struktura bioloških makromolekula,
prvenstveno proteina i nukleinskih kiselina kao što su DNA i RNA.
Struktura
DNA, odnosno njezina dvostruka uzvojnica otkrivena je na temelju
kristalografskih podataka. Struktura prve biološke makromolekule,
mioglobina,
određena je 1958. godine rendgenskom strukturnom analizom.
Rezultati
istraživanja struktura bioloških makromolekula prikupljeni su u Protein Data Bank
na adresi: http://www.rcsb.org/pdb/. Baza sadržava preko 163 000 struktura.
Ako malo
pročeprkate po toj stranici naći ćete mnogo korisnog znanja i
zanimljivih
sadržaja. Svakako pogledajte video "Kako enzimi rade" na adresi: https://www.rcsb.org/news?year=2018&article=5ab1131565eced58735888cb
Za
pretraživanje Protein Data
Bank (PDB) potrebno je više znanja. No, pokušat ćemo PDB
pretražiti imenom
našeg znanstvenika profesora dr. Nenada Bana koji od 2007. godine
djeluje kao
redoviti profesor na švicarskom
Saveznom
tehnološkom institutu (ETH) u Zürichu. ETH Zürich sedmo je sveučilište u svijetu s 31
Nobelovom nagradom. U tražilicu na vrhu stranice upišite Ban, N. i kliknite na Go.
Otvorit će vam se popis radova u kojima je Nenad Ban autor.
Pokušajmo
još jednom pretražiti PDB imenom prof. dr. sc
Dubravke Matković-Čalogović, redovite profesorice
u Zavodu za opću i anorgansku kemiju Prirodoslovno-matematičkog
fakulteta
Sveučilišta u Zagrebu. U tražilicu na vrhu stranice upišite Matkovic-Calogovic, D. i
kliknite na Go.
Odmah će vam se otvoriti dvadesetak radova u
kojima se kao autori pojavljuju naši znanstvenici Matković-Čalogović
Dubravka,
Prugovečki Biserka, Milić Dalibor, Đilović Ivica i drugi.
Odaberite 5NPY i
otvorit će se sljedeći podaci
za protein prikazan na slici 8.4.
Crystal structure of
Helicobacter pylori flagellar hook
protein FlgE2
DOI: 10.2210/pdb5NPY/pdb
Classification: MOTOR
PROTEIN
Organism(s): Helicobacter
pylori (strain G27)
Expression
System: Escherichia
coli BL21(DE3)
Deposited: 2017-04-19 Released: 2017-11-15
Deposition
Author(s): Loconte,
V., Zanotti,
G., Kekez,
I., Matkovic-Calogovic,
D.
Slika 8.5.
Kristalna struktura flagelne
kuke, proteina FlgE2 iz Helicobacter pylori, bakterije koja je uzročnik
čira
epitela želuca. Flagela (lat. flagellum - bič) je veliki kompleks
proteina koji
čini repić kojim se bakterija kreće (nanomotor) i kuku (hook) kojom se
pričvršćuje
za stijenku želuca. H. Pylori ima puno kompleksniju flagelu od drugih
bakterija
jer ima 2 različite kuke za razliku od ostalih koje imaju samo jednu. Izvor: https://febs.onlinelibrary.wiley.com/doi/full/10.1111/febs.14312
9.
Kristalografija je važna
Doznajte više na:
http://silverstripe.fkit.hr/kui/assets/Uploads/514-518.pdf
http://silverstripe.fkit.hr/kui/assets/Uploads/Osvrti-Kristalografija-217-218.pdfhttps://www.iycr2014.org/__data/assets/pdf_file/0008/93716/Crystallography_Hr_print.pdf
Nakon sto godina razvoja, rendgenska
kristalografija postala
je vodeća znanost koja proučava kristalnu strukturu i svojstva materijala.
Kristalografija je u središtu razvoja niza znanstvenih polja i
područja. Metodom
rendgenske strukturne analize do danas su određene kristalne
strukture više od milijun različitih spojeva. Navest ćemo samo nekoliko
primjera koji ukazuju na važnost kristalografije, ne samo za
tehnologiju, već i za ljudsko zdravlje. Primjerice, rendgenskom
strukturnom
analizom riješena je kristalna struktura inzulina,
hormona
koji regulira razinu šećera u krvi. Poznavanje kristalne strukture, a
to znači
poznavanje svih duljina veza i valentnih kutova, omogućilo je pak
sintezu
inzulina u laboratoriju. Prvu difrakcijsku sliku inzulina, tj. intenzitete
refleksa od mnoštva skupova mrežnih ravnina (hkl),
izmjerila je Dorothy Hodgkin (1910. –
1994.) još daleke 1935. godine. Tek su joj kompjutori početkom 1960-ih godina prošlog stoljeća
omogućili da nakon 35
godina rada na osnovi difrakcijske slike konačno 1969. godine odredi
kristalnu
strukturu inzulina. Za određivanje kristalnih struktura biološki važnih
molekula (penicilina, vitamina B12 i dr.)
Dorothy Hodgkin dobila je
Nobelovu nagradu za kemiju 1964. godine. Jedan od velikih uspjeha
rendgenske
strukturne analize je otkriće strukture DNA
(deoksiribonukleinske kiseline) koje se temelji na difrakcijskim
eksperimentima
što ih je izvela gotovo zaboravljena Rosalind Franklin (1920. –
1958.), koja je nažalost od raka prerano preminula. Nobelova nagrada se
ne dodjeljuje
posmrtno pa su Nobelovu nagradu za otkriće strukture DNA 1962. godine
dobili
James Watson, Francis Crick i Maurice Wilkins. Wilkins je bio suradnik
R.
Franklin koji je bez njezina znanja konkurentskom dvojcu Crick-Watson
prenosio
informacije o njezinim istraživanjima. Doznajte više na:
http://wellcomelibrary.org/collections/digital-collections/makers-of-modern-genetics/digitised-archives/rosalind-franklin/
https://wellcomelibrary.org/item/b1983116x#?m=0&cv=1&c=0&s=0&z=-0.9181%2C-0.0891%2C2.8364%2C1.7817
http://www.hazu.hr/kristalografi/kojic_100gxray.pdf
Kristalografija danas
Najvećim
uspjehom kristalografije u posljednje vrijeme možemo smatrati
otkriće kristalne strukture ribosoma,
multienzimatske strukture neophodne za odvijanje procesa sinteze proteina u
stanicama. Bez
ribosoma, stanica ne bi mogla
proizvesti nikakve proteine. Ribosomi se sastoje od dvije
podjedinice -
velike i male. Prvu kristalnu strukturu velikoga razlučivanja, 2,4 Å, (1 Å = 10–8 cm) velike 50S podjedinice ribosoma staničnog
organizma Haloarcula marismortui, metodom difrakcije rendgenskih
zraka riješio je još
2000. godine naš znanstvenik Nenad Ban
(1966.
– )
sa suradnicima. Godine 2014. objavio je trodimenzijsku strukturu 39S
velike
podjedinice svinjskog mitohondrijskog
ribosoma (vidi sliku
9.1.). Ribosomi su odgovorni za sintezu proteina u živim
stanicama, kako ljudskim, tako i biljnim te bakterijskim. Ako ribosomi
prestanu
funkcionirati, stanica ugiba. Ribosomi su glavne mete antibiotika.
Poznavanje
kristalne strukture bakterijskih i ljudskih ribosoma omogućuje
dizajniranje
novih antibiotika koji mogu napasti ribosome u štetnim bakterijama, a
da pri
tom oni u ljudskim stanicama ostanu neoštećeni. Doznajte više na:
https://www.sciencedirect.com/science/article/pii/S0092867402006190
http://science.sciencemag.org/content/289/5481/905)
http://www.znanostblog.com/otkrivena-detaljna-struktura-mitohondrijskog-ribosoma/
Slika
9.1. Prikaz polipeptidnih lanca i uzvojnica u kristalnoj strukturi
velike podjedinice mitohondrijskog ribosoma. (Prof. Nenad Ban i
suradnici / ETH
Zürich)
Izvor:
https://www.ethz.ch/en/news-and-events/eth-news/news/2014/01/mitoribosom.html
Venkatraman
Ramakrishnan, Thomas Steitz i Ada Yonath dobili su
Nobelovu nagradu za kemiju 2009. godine za proučavanje strukture i
funkcije
ribosoma.
Doznajte više na: https://www.nobelprize.org/nobel_prizes/chemistry/laureates/2009/illpres.html
U
ovo moderno doba, kad mnogo ljudi živi u velikim gradovima te se u
velikom broju okuplja na koncertima, utakmicama, prosvjedima
i
sličnim događanjima, pojavio se problem širenja zaraza. Najpoznatiji je
virus gripe koji stalno mutira pa se svake godine mora pripremati novo
cjepivo. Neke su zarazne bolesti, poput ospica, cijepljenjem gotovo
iskorinjene. No, pojavio se nekakav suludi pokret protiv cijepljenja pa
su se ospice ponovo pojavile. Slika 9.2. prikazuje kapsidu papiloma
virusa (HPV) za kojeg postoji efikasno cjepivo.
Slika 9.2.
a)
Model strukture kapside papilomavirusa (HPV). Struktura je riješena
metodom
krioelektronske mikroskopije (cryo-electron microscopy). Narančasto
označene
kapsomere okružuje pet kapsomera, a one u crvenoj boji okružuje šest
susjeda.
b) Prikaz strukture kapside papilomavirusa prekrivene specifičnim
antitijelima
(plavo). Na slici je prikazan samo dio antitijela uključenih u
strukturu.
Izvor: http://pdb101.rcsb.org/motm/221
Papilomavirus
je mali virus s jednostavnom
kapsidom koja okružuje kružni (cirkularni) DNA genom. Ovi virusi napadaju stanice u našoj koži i
sluznici. Infekcije
papilomavirusom uzrokuje dosadne bradavice, ali neke osobito virulentne
vrste
mogu uzrokovati rak vrata maternice. Srećom, postoji djelotvorno
cjepivo protiv
ovog virusa. Cjepivo je načinjeno od glavnog kapsidnog proteina virusa,
ali bez
DNA genoma unutar kapside. Imunološki sustav prepoznaje ovu praznu
ljusku i
potiče proizvodnju zaštitnih protutijela.
Nažalost,
za najnoviji korona virus COVID-19 nema
još cjepiva. U ovom svijetu
brzog i lakog putovanja samo u jednom danu virusi se mogu prenijeti
na sve kontinete i u sve države. Virusi lako mutiraju pa su
njihove mutacije postale sve veća opasnost za
svjetsko
zdravlje i ekonomiju. Najbolji su primjer koronavirusi koji su sa
svojih
prirodnih životinjskih domaćina prešli na čovjeka. Godine 2003., virus
SARS-a
pojavio se u Kini u populaciji šišmiša te prešao na ljude. Deset godina
kasnije, virus MERS također je sa slijepih miševa na Bliskom Istoku
prešao
najprije na jednogrbe deve, a potom i na ljude. Virus COVID-19,
zbog kojega su opustjele ulice u našim gradovima,
također se proširio s tržnice životinjama u Wuhanu u Kini.
Slika 9.3.
Glavna proteaza
korona virusa COVID-19 s inhibitorom u
tirkiznoj boji. Struktura je riješena metodom difrakcije rendgenskih
zraka. Proteaze
su oni enzimi
koji
kataliziraju
razgradnju
proteina hidrolizom peptidnih
veza koje
povezuju aminokiseline u
polipeptidnom lancu.
Poznavanje strukture
proteaza koristi znanstvenicima u potrazi
za spojevima koji blokiraju njihovo djelovanje. Ti se spojevi
potom koriste kao antivirusni lijekovi. No, raznolikost koronavirusa
uzrokuje
velike poteškoće u pronalaženju antivirusnih lijekova širokog spektra. Izvor:
PDB
Korona virusi
sadržavaju genom sastavljen od dugog lanca RNA - jednog od najvećih kod
svih RNA virusa. Ovaj genom djeluje poput glasničke
RNA.
U
inficiranoj stanici uzrokuje sintezu dva duga polipeptida potrebna pri
umnažanju
(replikaciji) novih virusa.
Korona virusne proteaze igraju bitnu ulogu u hidrolizi polipeptida
te su privlačna meta za dizajniranja antivirusnih lijekova.

Slika
9.4. Ove slike
prikazuju koronavirus u plućima, okružen sluzi koju izlučuju
respiratorne
stanice, izlučenim antitijelima i nekoliko proteina imunološkog
sustava. Virus
je zatvoren membranom koja uključuje S (spike) protein koji posreduje
pri vezanju
i ulasku virusa u stanice. M (membrane) protein uključen je u
organizaciju
nukleoproteina iznutra. E (envelope) protein čini membranski kanal u
ovojnici virusa.
Unutar ovojnice nalaze se mnoge kopije N (nucleocapsid) proteina
vezanog na
genomsku RNA. Ilustrirao David
S. Goodsell. Izvor: http://pdb101.rcsb.org/sci-art/goodsell-gallery/coronavirus
Nobelove nagrade
Tijekom
proteklih sto godina 50 znanstvenika dobilo je Nobelovu
nagradu za svoja otkrića koja su izravno ili neizravno povezana s
kristalografijom. Primjerice,
dobitnici Nobelove nagrade za kemiju za 2017. godinu su švicarac
Jacques
Dubochet, amerikanac Joachim Frank i britanac Richard Henderson.
Nagrada im je
dodijeljena za razvoj krioelektronske mikroskopije, revolucionarne
metode kojom
se pojednostavljuje i poboljšava vidljivost biomolekula. Ova metoda uvela je biokemiju u novo razdoblje jer znanstvenici
sada mogu zamrznuti biomolekule u pokretu i vidjeti procese koje nikada
ranije
nisu vidjeli, što je ključno za temeljno razumijevanje kemije života.
Krioelektronska
mikroskopija danas je dominantna metoda i ozbiljna alternativa
rendgenskoj
kristalografiji u rješavanju strukture bioloških makromolekula. O krioelektronskoj
mikroskopiji doznajte više
na: https://www.chemistryworld.com/news/explainer-what-is-cryo-electron-microscopy/3008091.article
https://www.nature.com/news/cryo-electron-microscopy-wins-chemistry-nobel-1.22738
https://hrcak.srce.hr/189651
https://www.youtube.com/watch?v=BJKkC0W-6Qk
Na jednom predavanju naš nobelovac Vladimir Prelog (1906. – 1998.) usporedio je klasične metode određivanja strukture molekula sa zamračenom prostorijom u kojoj se pipanjem pokušava doznati kako prostorija izgleda i što sadržava. Rendgenska strukturna analiza - to je kao kad uđete u prostoriju i upalite svjetlo. Drugim riječima, rendgenska strukturna analiza omogućila je kristalografima, kemičarima i molekulskim biolozima da "vide" atome, ione i molekule, da izmjere duljine kemijskih veza, izmjere valentne kutove, odrede apsolutnu konfiguraciju molekula i još mnogo toga.
Budućnost kristalografije
U današnje doba želimo otkriti tajne života. To je najveći izazov koji si čovjek može postaviti. Početne uspjehe već imamo. Znamo strukturu DNA. Doznali smo ljudski genom. Znamo strukturu ribosoma. Istražujemo strukture i funkciju virusa, enzima, proteina kako bismo bili uspješniji u borbi protiv mnogobrojnih bakterijskih i virusnih infekcija. U tim nastojanjima najviše nam pomaže kristalografija.
Na osnovi podataka što ih daje rendgenska strukturna analiza o međuatomskim udaljenostima i valentnim kutovima, možemo zaključivati o prirodi kemijske veze unutar molekula, međumolekulskim silama i interakcijama. Na osnovi tih spoznaja, pak, možemo razumjeti mnoga fizička i kemijska svojstva tvari, razumjeti procese koji se događaju u živim stanicama i tako razumjeti što je život i zašto je on uopće moguć. Rendgenska strukturna analiza pruža nam neposredne dokaze o putovima evolucije koja se i danas događa pred našim očima. Najbolji primjer za to su naše unaprijed izgubljene bitke s virusima i bakterijama. Čim pronađemo neki novi antibiotik kojim bismo "pobijedili" štetnu bakteriju, ona se promijeni i postane otporna na taj antibiotik. Zato se nemojte ljutiti ako vam liječnici ne daju antibiotike za svako vaše "curenje iz nosa" i slično.
Evolucija se ne može zaustaviti. Organizmi, tehnologije i društva koja ne evoluiraju zaostaju i nestaju s lica Zemlje.
Možda vas navedeni primjeri potaknu na avanturu studija prirodnih znanosti: fizike, kemije, biokemije, biologije, molekulske biologije, mineralogije ili geologije.
*****************************************
Preporučena
literatura za daljnje čitanje i učenje:
Lijep
pregled sadržaja iz opće kemije i svojstava krutina, s
primjerima i riješenim zadacima, naći ćete na adresi:
https://saylordotorg.github.io/text_general-chemistry-principles-patterns-and-applications-v1.0/s16-solids.html
Više
detalja o određivanju kristalnih struktura naći ćete na adresi: https://classes.soe.ucsc.edu/bme220/Spring07/NOTES/Xraycryst.IMcNae_MWalkinshaw.pdf
O
određivanju kristalnih struktura napisane su čitave biblioteke.
Jedna od takvih knjiga dostupna je na adresi: https://archive.org/details/springer_10.1007-978-3-662-06431-3
Ako
nemate dovoljno predznanja i živaca za čitanje knjige, proučite
magistarski rad na adresi:
https://www.research.manchester.ac.uk/portal/files/54503343/FULL_TEXT.PDF
Ako vas
zanima kristalografija proteina informacije potražite na
adresi:
http://www-structmed.cimr.cam.ac.uk/course.html
http://www.ruppweb.org/Xray/101index.html
https://pdb101.rcsb.org/learn/guide-to-understanding-pdb-data/dealing-with-coordinates
https://www.slideshare.net/martyynyyte/protein-structure-38028161
Ako vas
zanimaju računalni programi za pisanje strukturnih formula i
prikazivanje kristalnih struktura informacije potražite na adresi:
http://www.crystalmaker.com/software/index.html
**********************************
Zahvala
Autor izražava zahvalnost prof. dr. sc. Bogdanu Koturu, profesoru Sveučilišta u Lvovu, Ukraina, na vremenu i trudu uloženom pri čitanju prve verzije rukopisa, iskazanoj podršci te konstruktivnim razgovorima o ulozi Nikole Tesle i Ivana Puluja u otkriću rendgenskih zraka. Također zahvaljujem recenzentima na korisnim savjetima.
Pogovor
Na ovom
bi se mjestu trebao nalaziti popis upotrijebljene literature,
odnosno literaturni citati ili reference. No, njih nema. Naime, pri
pisanju ovog
udžbenika autor nije otvorio niti jednu tiskanu knjigu, rad ili
publikaciju. Pa
kako je nastao ovaj udžbenik? Većinom pomoću Interneta te "iz glave"
i na temelju vlastita iskustva. Ovaj je udžbenik zapravo uputa,
modernim rječnikom
"uputnik", kako pretraživati bespuća Interneta. Umjesto uobičajenih
literaturnih citata navode se URL adrese i poveznice prema izvorima
informacija. Bez Interneta teško bih došao do originalnih radova
objavljenih
prije više od stotinu godina, kao i do rezultata najnovijih istraživanja.
Kristalografskim
rječnikom rečeno, svaka je tiskana knjiga zatvorena
forma. Knjiga ima konačan sadržaj koji se izvan korica može proširiti
samo
posezanjem za sličnom drugom knjigom. No ovaj je udžbenik nešto poput sina
grčkog Boga Hermesa,
zaštitnika putnika i lopova, i
boginje Afrodite. S jedne strane to je udžbenik (knjiga),
a s druge kako već rekosmo uputnik, a može bit' i
uputnica
za putovanje Internetom. Čitaocu je prepušteno na volju. Može se
zadovoljiti
onim što piše u udžbeniku, ali u svakom trenutku može posegnuti za
sadržajima
navedenim pod "doznajte više". Možda je ovaj udžbenik nekakav
prijelazni oblik knjige, otvorena
forma koja se može proširivati onoliko koliko je to čitaocu potrebno
ili koliko
to sam želi. Evolucija je zakon pa i knjige ako žele preživjeti moraju
evoluirati iz zatvorene u otvorenu formu.
U
Zagrebu, proljeće 2020.
(Opaska.
Ovaj se udžbenik "kiselio" u ladici jednog nakladnika više od godine
dana. Kako
nije bilo izgledno da će biti tiskan u dogledno vrijeme, odlučio sam
objaviti
ga na e-skola kemija u rubrici udžbenici.)
Bilješka
o
autoru
Milan
Sikirica rođen 1934. u selu
Lučincima
pokraj Požege, umirovljeni je profesor Prirodoslovno-matematičkog
fakulteta
Sveučilišta u Zagrebu. Od osme godine živi, školuje se i radi u
Zagrebu. Pod
vodstvom prof. dr. sc. D. Grdenića diplomirao je 1959. godine na
Prirodoslovno-matematičkom
fakultetu Sveučilišta u Zagrebu s temom: Priprema
točkaste i slojne diode iz monokristala germanija. Doktorat znanosti
pod vodstvom prof. dr. sc.
D. Grdenića stekao
je 1963. godine na istom fakultetu s temom: Trokomponentni
sistemi urana, torija, molibdena i silicija. Oba su rada
izrađena u Odjelu
strukturne i anorganske kemije Instituta "Ruđer Bošković".
Od 1960.
do 1963. bio je asistent na Institutu "Ruđer
Bošković", a od 1963. do 1965. asistent u Zavodu za opću i anorgansku
kemiju Prirodoslovno-matematičkog fakulteta. Zvanje docenta stekao je
1965., za
izvanrednog profesora izabran je 1976., a redovnim profesorom postao je
1981. U
mirovini je od 2004. godine. Predavao je kolegije Opća
kemija, Anorganska kemija, Kemija čvrstog stanja i Metodika
nastave kemije.
Obnašao
je sljedeće važnije dužnosti: bio je tajnik Hrvatskog
kemijskog društva od 1969. do 1970., pročelnik Kemijskog odsjeka PMF-a,
prodekan Prirodoslovno-matematičkog fakulteta od 1982. do 1986., član
Prosvjetnog savjeta Hrvatske od 1983. do 1990. Dužnost predstojnika
Zavoda za
opću i anorgansku kemiju PMF-a obnašao je od 1984. do 1999.
Bavio se
istraživanjem kristalnih struktura međumetalnih i
organoživinih spojeva metodom rendgenske strukturne analize pa je iz
tog
područja objavio 50 znanstvenih radova i održao više od 70 predavanja
na
znanstvenim skupovima.
Intenzivno
se bavio problemima metodike nastave kemije pa je održao više
predavanja i seminara za nastavnike osnovnih i srednjih škola. Aktivno
je bio
uključen u proces uvođenja Hrvatskog
nacionalnog obrazovnog standarda (HNOS). Objavio je više
različitih
udžbenika i priručnika u izdanju Školske knjige od kojih se ističu: Stehiometrija (20 izdanja), Metodika nastave kemije, Zbirka
kemijskih pokusa za osnovnu i srednju
školu, te popularna zbirka 77 kuhinjskih pokusa za djecu i mlade od 7
do 77 godina. Krajem
2015. godine
objavio je besplatan cjeloviti digitalni udžbenik kemije za učenike 7.
i 8.
razreda osnovne škole (Milan Sikirica,
Mihaela Vrbnjak Grđan, Karmen Holenda, e-Kemija,
udžbenik za učenike osnovne škole) dostupan na adresi: http://eskola.chem.pmf.hr/udzbenik/web_Sikirica/index.htm.
Digitalni udžbenik sadržava niz poveznica prema drugim izvorima
informacija i 80
video uradaka u ukupnom trajanju od oko 8 sati. Video uradci dostupni
su na
adresi: https://www.youtube.com/channel/UCx4VyJfkV5Cfmj8datvi9Dw
Digitalni
udžbenik e-Kemija 1
za znatiželjne učenike
srednjih škola dostupan je na adresi: http://eskola.chem.pmf.hr/udzbenik/u102/index.html
Oženjen je, a supruga Đurđa podarila mu je dvije kćeri, Jelenu (1967.) i Paulu (1970.), a one pak četvero unučadi: Brunu (1997.), Lovru (1999.), Larinu (2003.) i Nevu (2006.).
